Волновые процессы в материальных средах: Учебное пособие, страница 3

Индексы v, h и d имеют дополнительные значения: V − вертикальные плоскости симметрии, h−горизонтальные, d− диагональные;

Т − набор осей симметрии кубического тетраэдра;

О − набор осей симметрии кубического октаэдра;

S− одна вертикальная зеркально-поворотная ось;

V − сочетание трех взаимно перпендикулярных осей 2-го порядка.

Таблица 2

Кристаллографические классы

Сингония	Международные символы и названия классов
	примитивный	центральный	планаль-ный	аксиальный	план-аксиальный	инвер- сионно- прими- тивный	инвер-сионнопланаль- ный
Триклинная	1
Моноклинная			m	2	2/m
Ромбическая			m m2	222	m m m
Тригональная	3		3 m	32	m
Тетрагональная	4	4/m	4mm	422	4/mmm		2m
Гексагональная	6	6/m	6mm	622	6/mmm		m2
Кубическая	3	m3	3m	432	m3m

В символах, предложенных академиком А.В.Шубниковым, оси nи плоскости m обозначаются так же, как и в международной символике. Перпендикулярность обозначается не чертой, а двоеточием, а параллельность − точкой. Косая черта, разделяющая два наименования осей, обозначает, что эти оси образуют между собой косой угол. Черта над символом оси означает, что эта ось является зеркально-поворотной осью.

1.4. Индицирование направлений и плоскостей в кристаллах

Если известны три основные трансляции , то положение любого узла в решетке определяется вектором:

,

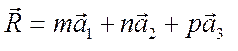где  m, n, p− целые числа.

Три числа m, n, p, заключенные в двойные квадратные скобки [[m, n, p]], называются символом узла.

Кристаллографическое направление − это направление прямой, проходящей по крайней мере через два узла решетки. Узел с координатами  [[000]]  принимается за начало координат.

Кристаллографическое направление полностью определяется узлом, ближайшим к началу координат.

Символ направления пишется в обычных квадратных скобках: [mnp]. Числа  m, n, p  называются индексами Миллера данного кристаллографического направления и всех параллельных ему направлений. Индексы Миллера записываются подряд, без запятых и читаются порознь. Например, [102] (один, ноль, два). Направления кристаллографических осей координат имеют индексы Миллера независимо от углов между осями координат: ось  X− [100], ось  Y− [010], ось Z  −  [001].

Совокупность направлений, которые могут симметрично совместиться друг с другом с помощью преобразований симметрии, свойственных данному классу симметрии, представляется в угловых скобках. Например, совокупность ребер куба á100ñ, пространственных диагоналей куба á111ñ, диагоналей грани куба á110ñ.

Если некоторые числа отрицательны, знак минус пишется над ними. Например, направление á10ñ читается так: один, минус один, ноль.

Положение плоскости однозначно определяется целочисленными отрезками, отсекаемыми ею на осях кристаллографических координат. Возможны три случая:

а) имеются три таких отрезка − плоскость не параллельна ни одной из осей координат;

б) плоскость параллельная одной из осей координат, она отсекает целочисленные отрезки на двух других осях;

в) плоскость параллельная двум осям координат − отрезок отсекается только на третьей.

Индексы Миллера записываются в круглых скобках (110). Координаторные плоскости обозначаются символами:

(100) − YOZ,  (010) − ZOX  и  (001) − ZOY

{hkl} − комплекс симметрично эквивалентных плоскостей, совокупность граней простой формы кристалла.

Чтобы полностью выявить симметрию кристаллов гексагональной  сингонии, используют четырехосную систему координат, т. е. в базисной плоскости, в дополнение к осям Xи Y, направленным по  и , вводится еще ось V, направленная по вектору −, −. По главной оси симметрии направлен вектор а₃ и соответственно ось Z.

Кристаллографические плоскости и направления обозначаются ориентировкой относительно всех четырех осей и четырьмя индексами, которые называются индексами Браве.

2. ПОНЯТИЕ  ТЕНЗОРА  И  ЗАКОНЫ  ПРЕОБРАЗОВАНИЯ
ЕГО  КОМПОНЕНТ

2.1. Векторы и скаляры

Величины, для определения которых достаточно знать одно число (положительное, отрицательное или нуль), называются скалярами. Это температура, плотность, масса, энтропия, теплоемкость, энергия.

Сравнивать можно только скаляры одинаковой размерности. Два скаляра одинаковой размерности равны, если их знаки и численные значения, получающиеся при измерении одной и той же единицы измерения, одинаковы.

В науке и технике чаще приходится оперировать величинами, для определения которых, кроме численного значения, необходимо указывать направление в пространстве: перемещение, скорость, ускорение, сила, напряжение электрического поля и т. д. Эти величины − векторы.

Скаляр и вектор – это не все классы величин, рассматриваемые наукой. Многие величины имеют более сложную структуру, чем векторы и скаляры, и для определения их недостаточно знать числовые значения и направления. Они называются тензорами (второго и высших рангов).

Так, для рассмотрения совокупности упругих напряжений на различных площадках в некоторой точке упругого тела необходимо понятие тензора упругих напряжений, а для исследования деформации произвольного элементарного объема упругого тела − понятие тензора деформаций.

2.2. Тензоры

Пусть электрическое поле, заданное вектором , действует на проводник; тогда по проводнику течет ток. Плотность тока (ток через единицу поверхности, перпендикулярной направлению тока) обозначим через вектор .

Если проводник изотропен и выполняется закон Ома, то вектор параллелен  и модуль  пропорционален модулю , поэтому , где s − удельная электропроводность.