Волновые процессы в материальных средах: Учебное пособие, страница 18

Уравнение 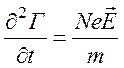 в длинноволновом пределе определяет ток в плазме, индуцированный полем в отсутствие магнитного поля. Если электрическое поле изменяется с частотой , то ток можно записать в виде

.

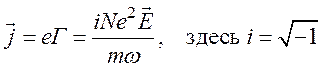Соответствующий вектор поляризации плазмы  определяется соотношением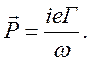

В этом случае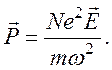

Проводимость плазмы σ и ее диэлектрическая проницаемость ε определяются соотношением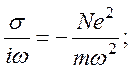

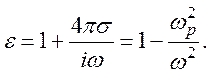
Существенно, что в отсутствие магнитного поля величина  отрицательна. Это означает, что смещение электронов сдвинуто по фазе на 180° по отношению к вынуждающему это движение полю.

Поэтому при ω<ω_pвеличина ε также отрицательна, и электромагнитные волны отражаются от такой среды полностью.

В немагнитной плазме  всегда отрицательно, поскольку электроны в такой среде полностью свободны. В замагниченной плазме магнитное поле оказывает сильное влияние на свойства плазмы. Основная причина состоит в том, что магнитное поле ограничивает движение в плоскости перпендикулярной направлению поля. В результате возникает удерживающая сила и характерная частота ω_c.

9. Частота рассеяния.

В твердых телах вследствие постоянно существующих тепловых колебаний решетки рассеяние всегда играет важную роль. Рассеяние носителей происходит на фононах, на ионизованных (резерфордовское рассеяние) и на нейтральных примесях. Значение в твердых телах измеряется от 10¹⁰до10¹³ c^-1 при возрастании температуры от температуры жидкого гелия (4,2 К) до комнатной (300 К).

10. Частота диэлектрической релаксации.

Еще одним важным параметром плазмы является частота диэлектрической релаксации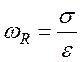, где σ – проводимость плазмы. Время диэлектрической релаксации τ_R- величина, обратная ω_R, в твердых телах имеет значение от 10^-18с в металлах до 10^-12с в большинстве полупроводников

11. Диффузия.

При конечной температуре в твердом теле пространственно неоднородное распределение носителей приводит к явлению диффузии, которое характеризуется коэффициентом диффузии

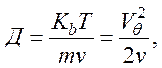
где V_θ – средняя тепловая скорость.

Для большинства твердых тел в условиях, представляющих технический интерес, V_θ≈10⁶ м/с, v=10¹³ c^-1 и Д = 10^-1 м²/с.

Диффузия накладывает верхний предел на частоту различных возмущений. Если V_ф фазовая скорость волны, то по определению диффузионной частоты 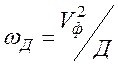, и тогда частота волны будет ограничена неравенством

ω²<ω_RД.

Это ограничение эквивалентно следующим требованиям:

где λ>λ_Д,где λ - длина волны; τ_Д>τ_R, где τ_Д – время, необходимое для диффузии носителей на расстояние, равное длине волны;τ_R – время диэлектрической релаксации

6.4. Основные уравнения состояния плазмы

В плазме нас интересует ее коллективный отклик на электромагнитные и другие виды возмущений. Этот отклик определяется суммарным действием

микропроцессов в плазме.

Если выполняется условие (75), то для описания волн в объеме плазмы будем использовать уравнения Максвелла для среднестатических величин электрического и магнитного поля в среде:

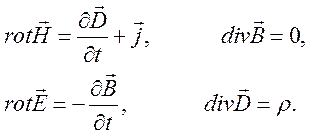                                                                                                    (78)

Полная система уравнений, позволяющая найти отклик плазмы на заданное возмущение, образуется из уравнений (78) для полей, дополненных уравнениями для токов j или зарядов q, которые должны включать в себя параметры плазмы и все виды сил, действующих на частицы в плазме. Нахождение токов в плазме из уравнений движения для каждой отдельной частицы плазмы задача практически неразрешимая. Поэтому для определения микроскопического тока в плазме используются различные приближения: приближение отдельных частиц, гидродинамическое приближение, приближение кинетического уравнения.

6.5. Приближение отдельных частиц

По этому приближению заряженные частицы плазмы заданного вида под действием внешних сил дрейфуют независимо друг от друга с одинаковыми скоростями, которые находятся из уравнения движения для отдельной частицы:

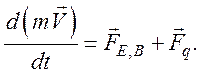                                                                                                    (79)

здесь - силы электромагнитного происхождения: - силы неэлектромагнитного происхождения. Электромагнитная сила есть сила Лоренца:

                                                                                                    (80)

Наличие сил не электромагнитного происхождения обусловлено главным образом столкновениями частиц плазмы с кристаллической решеткой, частота которой (v_p от 10¹² до 10¹³c^-1):

                                                                                                    (81)

где v_p – средняя частота столкновений частиц плазмы с решеткой, при которых изменяется средний по ансамблю частиц дрейфовый импульс . Подставив (80) и (81) в (79), получим

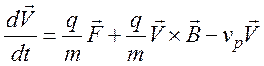                                                                                                    (82)

– уравнение движения.

Найденная из (82) дрейфовая скорость частиц определяет дрейфовый ток в плазме:

                                                                                                    (83)

Уравнения (78) совместно с (82) и (83) образуют полную систему уравнений, позволяющих найти отклик плазмы в приближении отдельных частиц.

Если в плазме имеется несколько видов подвижных частиц, то уравнения движения (82) записываются для каждого вида отдельно, а дрейфовый ток частиц определяется как сумма парциальных токов частиц каждого вида.

6.6. Приближение кинетического уравнения

Для нахождения токов и зарядов в плазме используют статический метод, рассматривающий ансамбль частиц в целом:

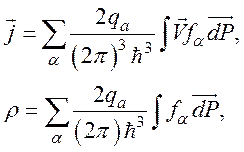
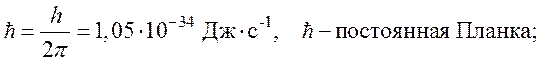
h=6,625×10^-34 Дж c^-1,

где суммирование проводится по всем α видам частиц.

6.7. Гидродинамическое приближение

Подвижные носители заряда в плазме рассматриваются как некоторая сплошная среда,- проводящая жидкость, помещенная в кристаллическую решетку. Предполагается при этом, что скорости частиц плазмы могут принимать самые различные значения, но в пределах некоторого микроскопического элемента жидкости (называемого жидкой частицей) устанавливается определенное распределение частиц по скоростям, которому соответствует определенная средняя скорость.

Для нахождения электрических токов и потоков вещества в плазме записывается уравнение движения для жидких частиц. Если плазма содержит подвижные частицы лишь одного вида, то уравнение движения имеет вид