Волновые процессы в материальных средах: Учебное пособие, страница 21

Получим эту форму записи уравнений Максвелла. Гармоническую волну записываем в виде

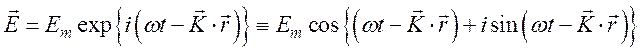                                                                                                    (99)

Физический смысл будет иметь реальная часть уравнения (99).

Оператор Гамильтона в декартовых координатах имеет вид

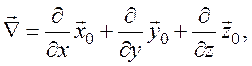
 а функции –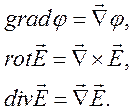   

Здесь – единичные векторы направлений декартовых координат.

Отсюда

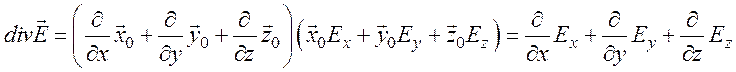                                                                                                  (100)

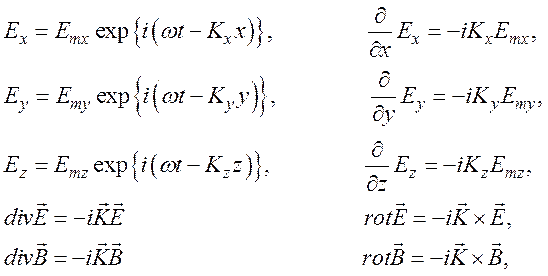                                                                                                  (101)

т. е.   

Временные производные

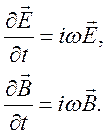                                                                                                  (102)

Подставим (100), (101), (102) вместо соответствующих членов в уравнения Максвелла

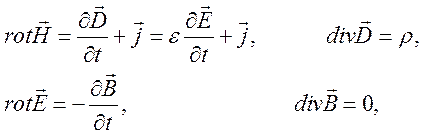
получим

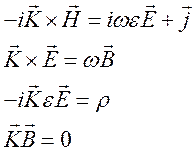
Рассмотрим более подробно этот переход на примере  для первого уравнения:

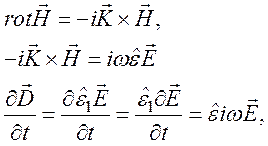
откуда  

Аналогично получаем второе уравнение

.

Сократив на –i, получим

.

8. Электромагнитные  волны  в  ПЛАЗМе  ПОЛУПРОВОДНИКОВ

8.1. Характеристические уравнения

Исследование распространения электромагнитных волн в плазме полупроводников будем проводить, используя систему уравнений Максвелла, при этом будем полагать, что среда однородная, бесконечная и немагнитная, т.е. . С учётом этого система уравнений будет иметь вид

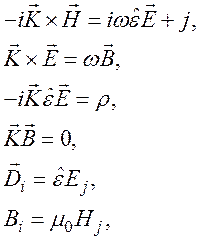                                                                                                  (103)

где  – тензор диэлектрической проницаемости второго ранга.

Получим вначале дисперсионные соотношения для монохроматических волн в плазме в отсутствии постоянного поля  и связанного с ним дрейфа носителей заряда. Из дисперсионного уравнения найдём характеристики распространения волн: затухание амплитуды в пространстве, поляризацию волны, фазовую скорость, диапазоны частот, с которыми волны могут распространяться в плазме.

Запишем основные формулы, характеризующие распространение слабозатухающей монохроматической плоской волны вида

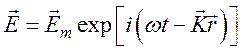
для случая, когда                                                   ,

длина волны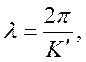                                                          

фазовая скорость волны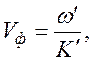                                       

коэффициент затухания амплитуды волны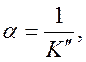        

показатель преломления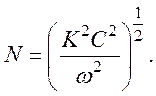                                      

Здесь K' и K''– действительная и мнимая части волнового числа, а
K – его модуль. Коэффициент отражения для случаев нормального падения фронта волны на поверхность

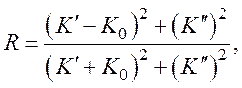
где 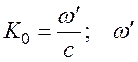 – действительная часть комплексной частоты.

Эти величины и их зависимость от частоты волны найдём, решая систему уравнений Максвелла (103).

Решения системы уравнений (103) будем искать для гармонических плоских волн вида

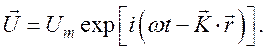
Продифференцируем уравнение (1) системы (103) по времени и заменим в уравнении вектор  на , тогда получим

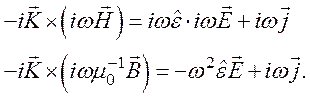
После сокращения получим

                                                                                                  (104)

Из уравнения (2) системы (103) выразим :

и подставим в (104):

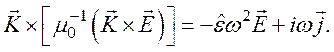
Умножим на μ₀ левую и правую части:

Получим 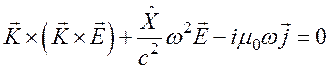                            (105)

Где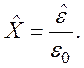   

Рассматривая задачу в линейном приближении, полагаем, что

где  – тензор дифференциальной проводимости. Запишем это уравнение в матричном виде:

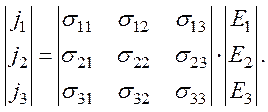                                                                                                  (106)

Подставив (106) в (105), получим систему уравнений

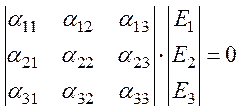
или      .                    (107)

Компоненты α_ij имеют вид

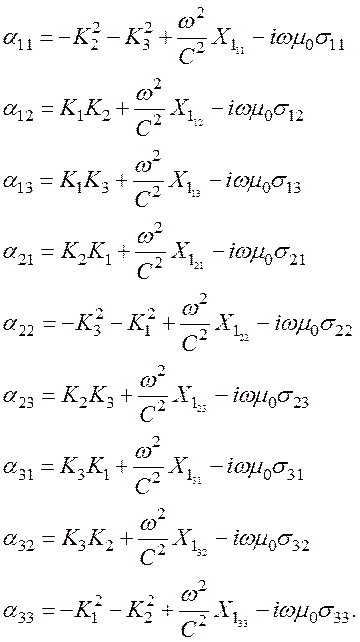
Как показывает анализ, уравнение (107) есть однородное полевое уравнение. Нетривиальными будут его решения, когда детерминант будет равен нулю, т. е.

                                                                                                  (108)

Уравнение (108) определяет дисперсионное соотношение, устанавливающее связь между ω и :

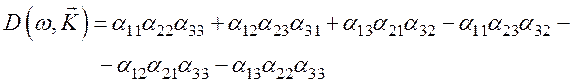                                                                                                  (109)

Компоненты тензора проводимости σ_ij, которые входят в дисперсионное уравнение (109), находят из уравнения для тока (106), которое в гидродинамическом приближении определяется уравнением движения.

Дисперсионное уравнение (107) довольно громоздко, однако при решении конкретных задач за счёт подбора системы координат удаётся значительно его упростить.

Далее будем рассматривать раздельно-продольные волны, у которых , и поперечные  волны.

Поперечные волны обычно называют электромагнитными или вихревыми . Поэтому они в соответствии с уравнениями (103) сопровождаются магнитными полями.

Продольные волны не обладают магнитной компонентой, т. е.  их возникновение связано с образованием объёмных зарядов, о чём свидетельствует скалярное произведение

Эти волны называют безвихревыми, или потенциальными, и их волновое уравнение из (105) найдем путём простого преобразования:

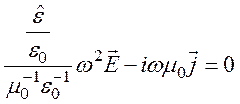
или                  (110)

Умножая уравнение (110) скалярно на  и учитывая уравнения (4) и (3) из (103), получаем уравнение

которое называется уравнением непрерывности тока.

8.2. Продольные волны в холодной плазме

Будем рассматривать распространение волн в холодной неограниченной плазме в отсутствии магнитного поля  в направлении оси x₃.

В линейном приближении при  определитель волнового уравнения (108) будет содержать только диагональные компоненты α₁₁, α₂₂, α₃₃, а остальные компоненты будут равны нулю. Волновое уравнение (107) в этом случае имеет вид

α₃₃Е₃₃=0,                                                                                                   (111)

поскольку Е₁= Е₂=0 и K₁= K₂=0.

В холодной плазме σ₃₃ не зависит от волнового вектора , и уравнение (109) не является дисперсионным, поскольку в нём нет . Физически это соответствует тому, что распространения колебаний плазмы не происходит, при этом возможны два случая:

 столкновительный, когда                    ωτ_p<<1;

 бесстолкновительный, когда               ωτ_p>>1.

Для первого случая σ₃₃- действительная величина. Из (111) получим ω'=0. Следовательно, периодические колебания отсутствуют, а возмущения в плазме экспоненциально затухают с постоянной затухания