Волновые процессы в материальных средах: Учебное пособие, страница 13

Таким образом, в общем случае уравнение (21) будет иметь пять корней: а_j= 1, 2,..., 5, расположенных в нижней комплексной полуплоскости, которые соответствуют бегущим вдоль оси x₁ волнам и удовлетворяют условию затухания на глубине.

Связь между различными а_j, определяющими одну моду поверхностной волны, находится из граничных условий. Составим линейную комбинацию из пяти членов вида (18), описывающих поверхностные волны, каждая из которых имеет одинаковую фазовую скорость, но разные значения а_j, равные корням уравнения (21). Тогда решение примет вид

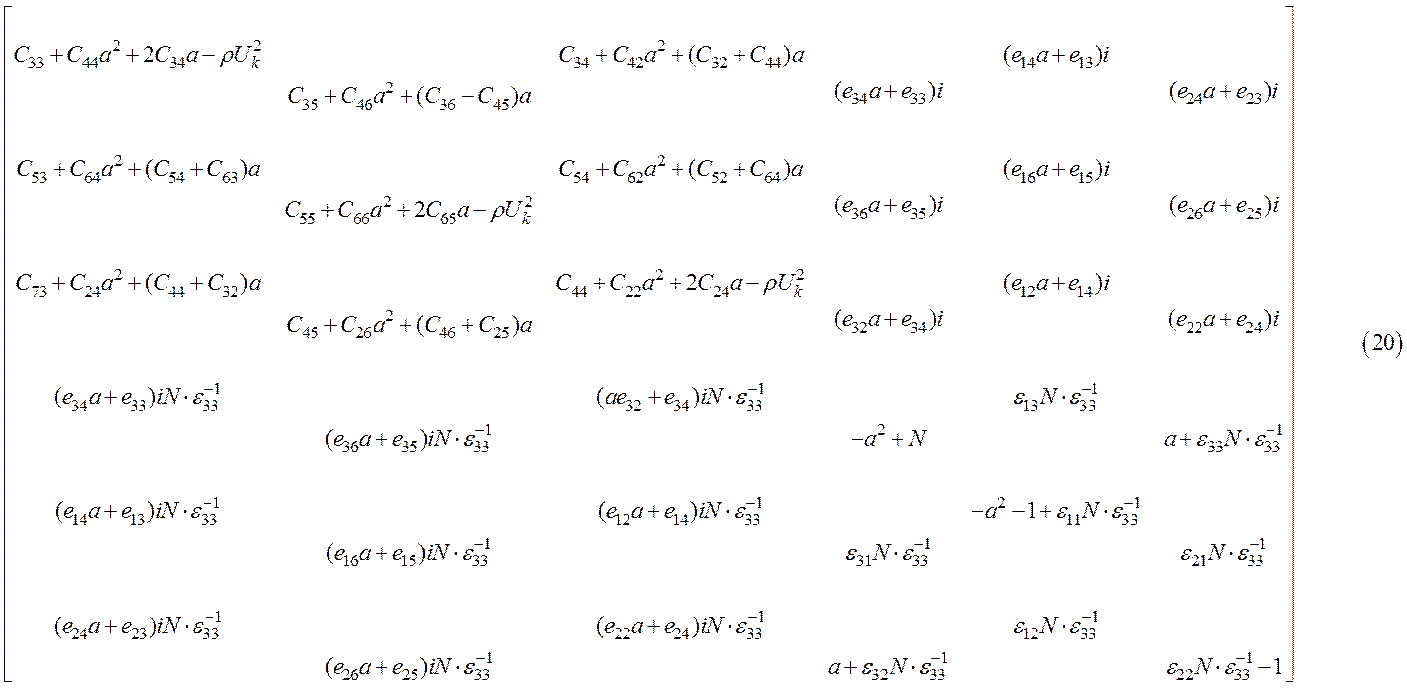
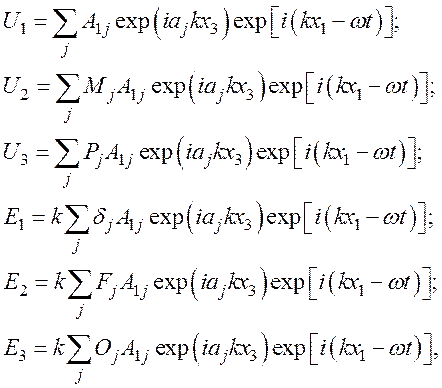                                                                                                                      (22)

где .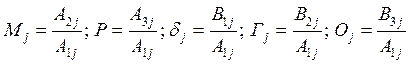

Эти решения должны удовлетворять следующим граничным условиям:

1. На свободной поверхности пьезоэлектрика отсутствуют упругие напряжения, т.е.

.                                                                                                    (23)

2. На границе кристалла с вакуумом непрерывны нормальная составляющая вектора магнитной индукции, тангенциальные компоненты электри`ческого и продольная компонента магнитного полей:

                                                                                                    (24)

                                                                                                    (25)

H₁(0-)=H₁(0+),                                                                                                    (26)

где (0-) и (0+) обозначают соответствующую компоненту в кристалле и вне кристалла.

Поскольку электромагнитное поле на границе кристалла с вакуумом должно быть непрерывно, то для x≥0 можно записать, что

.                                                                                                    (27)

Подставив выражения (27) в волновое уравнение для свободного пространства , получим

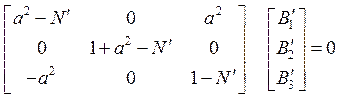                                                                                                    (28)

где 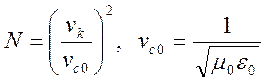 - скорость света в свободном пространстве.

Из второго уравнения (28) найдем значение константы затухания электрического поля в вакууме:

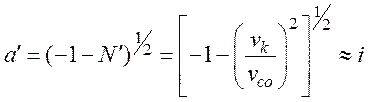,                                                                                                    (29)

поскольку величина .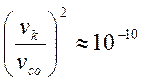

Из уравнения (12) найдем :

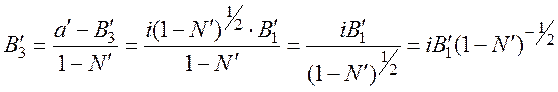.                                                                                                    (30)

Подставив в уравнение (23) значения для U_i и E_i из (22). После дифференцирования получим

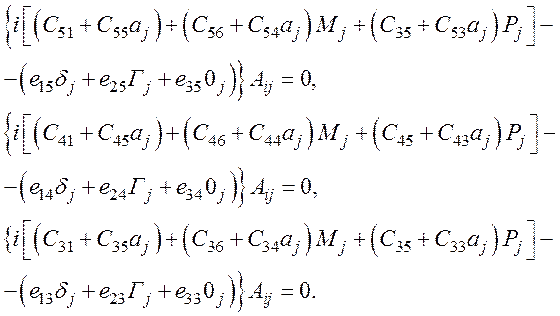                                                                                                    (31)

Обратимся к граничному условию (25). Запишем значение , подставив в уравнение (25) значения для U_i и E_i из (22), а для E₃(0+) из (27):

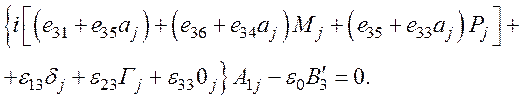                                                                                                    (32)

Рассмотрим граничные условия (24)

 и .

Записав значения компонент, получим:

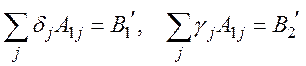.                                                                                                    (17)

Введем значения  из (33) в (30), а последнее – в (32).

После всех преобразований получим

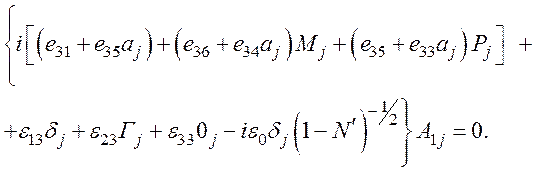                                                                                                    (34)

Рассмотрим граничные условия (26)

H₁(0-)=H₁(0+).

Из уравнений Максвелла имеем:

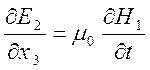.                                                                                                    (35)

Поставив значения Е₂ и Е₃ для кристалла (22) и вакуума (27) в значение (35), получим для магнитных компонент

,

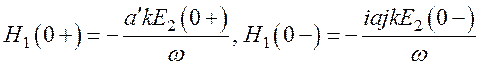или для граничных условий (26) имеем

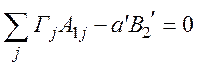.                                                                                                    (36)

Записав в уравнение (36) значение  из (29) и значение  из (33), окончательно найдем

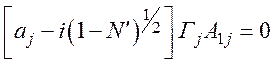.                                                                                                    (37)

Уравнения (31), (34), (37) сведем в систему:

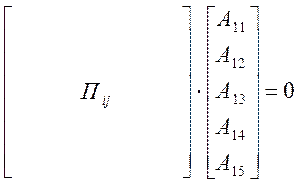.                                                                                                    (38)

Компоненты  запишем в виде

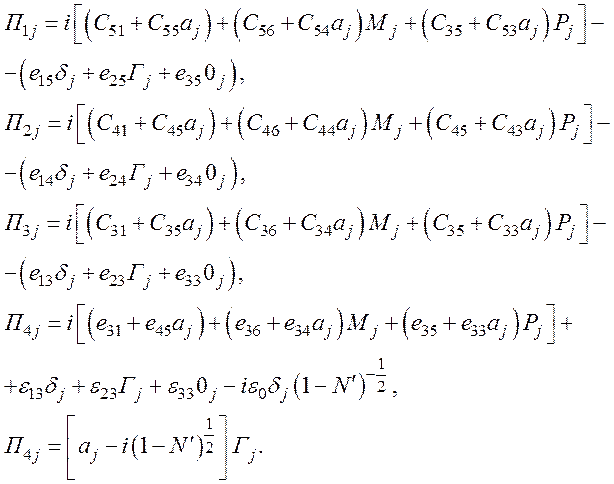                                                                                                    (39)

Как уже упоминалось в (21), необходимым условием существования нетривиального решения этой системы является обращение в нуль определителя системы:

.                                                                                                    (40)

Задаваясь численными значениями фазовой скорости волны и решая совместно определители (21) и (40), можно найти все коэффициенты, входящие в уравнения (22), для компонентов волны.

Определим отношение амплитудных коэффициентов уравнений (22):

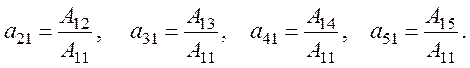
Тогда получим окончательные выражения для механических смещений и электрических полей в следующей форме:

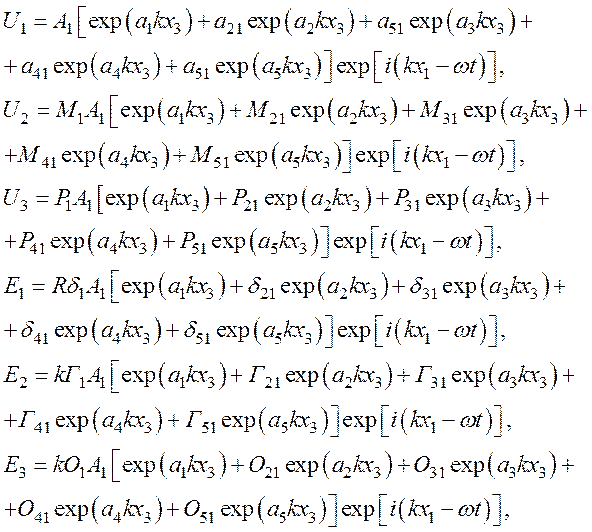
где

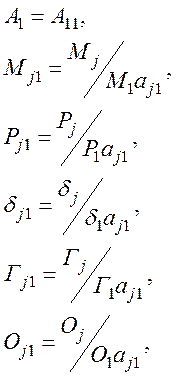
Подставляя в выражения (21) и (39) материальные тензоры, соответствующие определенному срезу исследуемого кристалла, найдем характеристические уравнения поверхностных волн, которые распространяются в этом срезе кристалла вдоль оси х₁. Для получения характеристических уравнений поверхностных волн другого направления распространения необходимо в уравнениях (21) и (39) произвести замену индексов материальных тензоров в соответствии с выбранной координатной системой.

При подстановке материальных тензоров в частном случае характеристические уравнения (21) разбиваются на два набора уравнений, соответствующих поверхностным волнам различного типа. Порядок характеристического уравнения при этом понижается, и уравнения принимают более простой вид.

Выражения (21) и (39) пригодны для анализа поверхностных волн как для кристаллов произвольной симметрии, так и поликристаллических сред, электромеханические свойства которых описываются модулями упругости С, пьезоэлектрическими постоянными e и диэлектрической проницаемостью ε.

5. ПОВЕРХНОСТНЫЕ ВОЛНЫ В СЛОИСТЫХ
ТОНКОПЛЕНОЧНЫХ СРЕДАХ

5.1. Характеристические уравнения для поверхностных волн,
 распространяющихся в слоистых тонкопленочных средах