Волновые процессы в материальных средах: Учебное пособие, страница 2

Поскольку симметрия внешней формы кристалла отражает симметрию его структуры, кристаллографическую систему координат выбирают по ребрам кристаллического многогранника. В общем случае − это косоугольные координатные системы с неодинаковыми масштабными отрезками по осям. Они хорошо согласуются с симметрией кристалла и существенно упрощают его аналитическое  описание. Именно этот способ выбора координатных систем лежит в основе разделения кристаллов на сингонии. В сингонию (см.
рис. 2) объединяются кристаллы, у которых одинакова симметрия элементарных ячеек их структур и одинакова кристаллографическая система осей координат.

Рис. 2. Кристаллографические системы координат

и кристаллографические сингонии: а - общая, б – триклинная,
в – моноклинная, г – ромбическая, д – гексагональная,
е – тригональная, ж – тетрагональная, з – кубическая,
т – нормаль, 2, 3, 4 и т.д. – оси симметрии

Симметрия формы кристаллов и их физических свойств есть характерная особенность кристаллов, которая описывается с помощью элементов симметрии.

Симметричной называется такая фигура, которая может совместиться сама с собой в результате симметричных преобразований или операций. Такими операциями являются операции отражения и вращения, позволяющие при их осуществлении совмещать фигуру саму с собой.

Воображаемые плоскости, линии и точки, с помощью которых осуществляются эти отражения и вращения, называются элементами симметрии.

Для обозначения симметричных преобразований и соответствующих им элементов в кристаллографии пользуются условными символами (см.
табл. 1). Плоскость симметрии − плоскость, которая делит фигуру на две части, расположенные друг относительно друга как предмет и его зеркальное отражение.

Таблица 1

Элементы симметрии конечных фигур и их обозначения

Название	Международный символ
Плоскость симметрии	m
Центр симметрии
Поворотная ось:    двойная    тройная    четверная    шестерная	n 2 3 4 6
Инверсионная ось симметрии:    тройная    четверная    шестерная

Например, в кубе имеется девять плоскостей симметрии: три взаимно перпендикулярные плоскости, которые делят пополам противоположные ребра куба, и шесть плоскостей, проходящих по диагоналям граней куба. Все девять плоскостей пересекаются в центре куба.

Осью симметрии называется прямая линия, при повороте вокруг которой на некоторый определенный угол фигура совмещается сама с собой. Порядок оси симметрии nпоказывает, сколько раз фигура совместится сама с собой при полном обороте вокруг этой оси.

Центр симметрии (центр инверсии) − особая точка внутри фигуры, характеризующаяся тем, что любая прямая, проведенная через центр симметрии, встречает одинаковые (соответственные) точки фигуры по обе стороны от центра на равных расстояниях.

Полярным называется направление, концы которого геометрически и физически не эквивалентны.

Отражение в плоскости, поворот вокруг оси симметрии, зеркальное отражение в центре симметрии представляют собой конечные, или точечные, симметричные преобразования. При этих преобразованиях фигура не перемещается как целое и хотя бы одна ее точка остается на месте. В кристаллах возможны только оси симметрии 1, 2, 3, 4, 6-го порядка и не существует осей симметрии 5-го порядка и порядка, большего, чем 6. Это ограничение обусловлено тем, что кристаллическое вещество − бесконечная система материальных частиц, симметрично повторяющихся в пространстве. Такие симметричные бесконечные ряды, сетки, решетки, непрерывно заполняющие пространство, несовместимы с осями 5, 7-го и других, более высоких порядков.

Совокупностью  m  2, 3, 4, 6,

                            P, L₂, L_3, L₄, L₆

 исчерпываются все возможные в кристаллах конечные операции симметрии 1-го рода.

Конечные операции симметрии 2-го рода представляют собой совместное действие двух операций симметрии: вращение и инверсия в центре симметрии или вращение и отражение в плоскости симметрии.

Инверсионная ось симметрии представляет собой сочетание оси вращения и одновременного отражения (инверсии) в центре симметрии. Инверсионные оси обозначаются следующим образом:

  или  .

Зеркально-поворотная ось симметрии представляет собой сочетание оси симметрии и отражения ее в плоскости симметрии, перпендикулярной этой оси.

1.3. Кристаллографические классы и системы их обозначения

Все многообразие естественных и искусственных кристаллов можно представить 32 кристаллографическими классами, которые объединены в семь сингоний (см. табл. 2).

Классом симметрии кристаллов называется полная совокупность элементов симметрии или возможных симметричных преобразований этого объекта. Каждый из 32 классов симметрии обозначается специальным символом, в котором условно записана формула симметрии кристалла. В настоящее время используются несколько систем обозначения классов симметрии. Наиболее употребительны международные (интернациональные символы, символы Шубникова и символы Шенфлиса).

В международном символе класса записываются только основные элементы симметрии или порождающие, в качестве которых используются плоскости симметрии кристаллов. В международной символике приняты следующие обозначения:

n − ось симметрии n-го порядка;

 − инверсионная ось симметрии n-го порядка;

m− плоскость симметрии;

nm− ось симметрии n-го порядка и mплоскостей симметрии, проходящих вдоль нее;

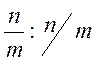 − ось симметрии n-го порядка и перпендикулярная ей плоскость симметрии;

n2 − ось симметрии n-го порядка и nосей 2-го порядка, ей перпендикулярных;

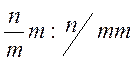 − ось симметрии n-го порядка и плоскости m, параллельные и перпендикулярные ей.

nи  могут иметь значения 1, 2, 3, 4, 6.

В символах Шенфлиса, часто используемых в кристаллофизической литературе, применяются следующие обозначения:

С − одна ось симметрии;

D− ось симметрии и оси 2-го порядка, перпендикулярные ей. Единственная ось всегда считается вертикальной. Если осей несколько, то вертикальной считается ось высшего порядка.