Волновые процессы в материальных средах: Учебное пособие, страница 22

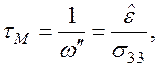
где τ_M – время диэлектрической релаксации (Максвелловское время релаксации). Это можно показать, используя (107):

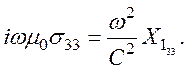
значит,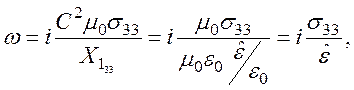   

т. е. получили мнимую частоту ω''. Физически это свидетельствует о том, что заряды в плазме, разведённые полем в пространстве, устремляются друг к другу, но вследствие трения (столкновениями в решётке) затормаживаются и колебаний не возникает.

В случае отсутствия столкновений, и движение зарядов друг к другу вследствие инерции приводит к перелёту или новому разделению. Это приводит к колебательному процессу, а σ₃₃ будет мнимой величиной, равной

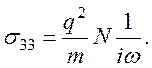                                                                                                  (112)

Подставив (112) в (111), получим

ω'=ω_p,

где 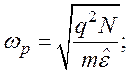 ω_p – плазменная или Ленгмюровская частота. Численное значение её

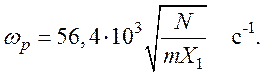
Здесь N выражено в см^-3, а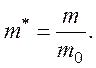

Плазменная частота ω_p – важнейший параметр плазмы. С этой частотой совершаются колебания отрицательных зарядов относительно положительных. Квант энергии плазменных колебаний называется плазмоном. В полу- проводниках ћ ω_p~10^-3 эВ, что соответствует энергии тепловых колебаний электронов.

Плазменная частота и максвелловское время релаксации связаны соотношением

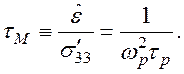
Таким образом, продольные волны в незамагниченной  плазме не распространяются, в плазме могут существовать плазменные колебания с частотой ω_p, когда столкновения зарядов с решёткой отсутствуют.

8.3. Поперечные волны в плазме

При условии, что волны распространяются в направлении оси , т. е. K₃≠0, Е₃=0, K₁= K₂=0 , дисперсионное уравнение (108) имеет вид

α₂₂= α₁₁=0.

Считаем, что полупроводник изотропен, σ₁₁= σ₂₂= σ и преобразуется к виду

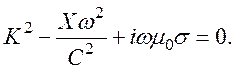                                                                                                  (113)

Для бесстолкновительного случая, когда ωτ_p>>1, подставив (112) в (113), получим

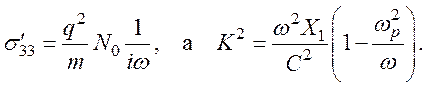                                                                                                  (114)

В уравнении (114) использовали значение для

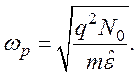
Проанализируем выражение (114). Если ω<ω_p, то K₂<0 или K'<0. Это означает, что в плазме не возбуждаются поперечные волны с частотами, меньше плазменной частоты.

Волны с частотами, меньше ω_p, полностью отражаются от плазмы, поскольку коэффициент отражения

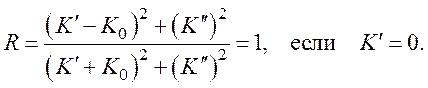
Равенство R единице соответствует непропусканию волн. Физически это означает, что носители в плазме успевают перераспределиться таким образом, что экранируют проникновение волн в плазму. Глубину переходного слоя α найдем по формуле

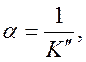
α – это величина, на которой амплитуда падающей волны затухает в eраз. Если 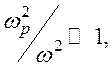 то согласно (114)

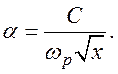
Отметим, что затухание волн происходит не за счет рассеяния энергии, а за счет индуцирования обратной волны. В этом заключается отличие непропускания волн от их поглощения.

Если ω>ω_p, то K₂>0, значит, в бесстолкновительной плазме могут распространяться незатухающие волны (K'≠0, K''=0). Фазовая скорость проникающей волны определяется по формуле

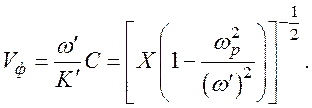
Как показывает анализ этой формулы, фазовая скорость больше скорости света в среде с решеточной диэлектрической проницаемостью X. Это указывает на то, что свободные носители вносят отрицательный вклад в диэлектрическую постоянную.

Если ω=ω_p, то V_ф→∞, а групповая скорость

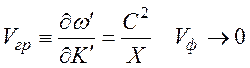
Этот случай соответствует резонансному раскачиванию собственных колебаний плазмы, а ток смещения будет равен дрейфовому току свободных носителей. Эти токи в соответствии с уравнением непрерывности направлены противоположно, а суммарный ток в плазме будет равен нулю:

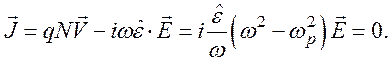
Определим глубину проникновения волны 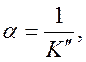 для чего учтем столкновение носителей с центрами рассеяния, которые и являются физической причиной обуславливающей потери энергии волн.

В твердых телах τ_p~10^-13сек. Уравнение, определяющее столкновительный случай, будет удовлетворяться во всем радиотехническом диапазоне. Проводимость плазмы σ будет действительной величиной. Волновой вектор  будет носить комплексный характер. Его действительную и мнимую части определим из (113):

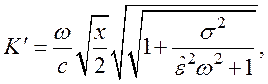                                                                                                  (115)

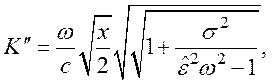                                                                                                  (116)

Для хорошо проводящих сред

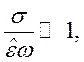
т. е. ток проводимости σ  больше токов смещения,  а

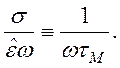
Значит,

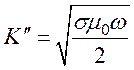                                                                                                  (117)

и

K'=K''.

Положительный корень K в уравнении (117) следует отбросить, так как нет физических причин, которые могут передать в рассматриваемом случае энергию волне, поэтому выбираем корень K''<0, определяющий затухание.

Глубину, на которой амплитуда волны затухает в e раз, определяется выражением

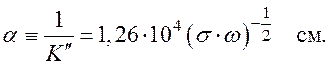
Здесь σ измеряется в Ом^-1см^-1.

Если токи смещения больше токов проводимости, то

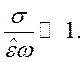
из (115) и (116) получим

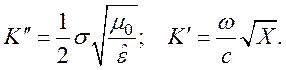
Подставив значение σ (Ом^-1см^-1), получим

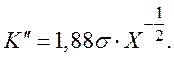
Таким образом, в холодной неограниченной плазме электромагнитные волны не распространяются. Возможны только нераспространяющиеся плазменные колебания в достаточном малом ограниченном объеме.

8.4. Электрокинетические волны в плазме полупроводников

Рассмотрим поведение плазмы, когда на нее воздействует постоянное электрическое поле , либо постоянное магнитное поле , либо они воздействуют одновременно.

В такой полевой геометрии возможно существование распространяющихся волн различной структуры и параметров, представляющих интерес для использования в устройствах обработки информации.

Анализ этих волн будем проводить на основе системы уравнений Максвелла (103), которая должна быть дополнена уравнением движения, уравнением непрерывности, а также материальными уравнениями:

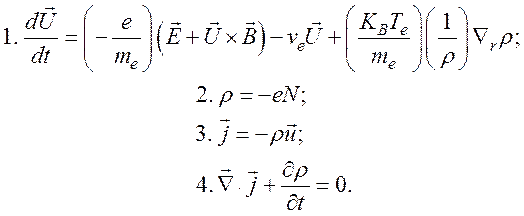                                                                                                  (118)

Рассмотрим линейный отклик электронной плазмы, т. е. плазмы, у которой свободными носителями являются электроны, на гармоническое во времени и пространстве электромагнитное возмущение вида (99).

При этом плазму будем характеризовать тензором диэлектрической проницаемости 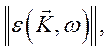 в котором отражена пространственная и частотная дисперсия и который имеет следующий вид при воздействии на плазму внешнего магнитного поля :