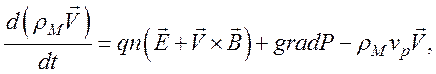Волновые процессы в материальных средах: Учебное пособие, страница 19

                                                                                                    (83)

где ρ_M=mN – плотность жидкой частицы; – средняя скорость ее;
P –давление (силы давления в плазме обусловлены тепловым хаотическим движением частиц); P=P(ρ_M,T) – уравнение состояния (84):

P = NK_bBT_n – уравнение переноса тепла                                                                                                    (85)

T_N – температура подвижных частиц.

Полная система уравнений плазмы в гидродинамическом приближении образуется, если дополнить уравнение (78) и (83) уравнением состояния (84) и уравнением переноса (85).

Система гидродинамических уравнений значительно упрощается если можно пренебречь силой, связанной с тепловым давлением.

В этом приближении, которое называется приближением холодной плазмы, уравнение (83) преобразуется к виду

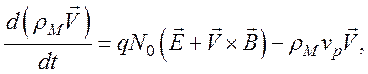                                                                                                    (86)

схожему с уравнением движения в приближении отдельных частиц.

Уравнения (78) и (86) образуют полную систему уравнений холодной плазмы.

Если силы, обусловленные градиентом теплового давления в плазме, сравнимы или больше сил электромагнитного происхождения, то плазму называют горячей.

Условием применимости гидродинамического приближения является неравенство

λ>>l_M,

где l_M – минимальный размер жидкой частицы, который определяется характерными длинами свободных пробегов частиц между разного рода столкновениями с потерей импульса, а также энергии.

Кроме того, при гидродинамическом приближении обычно в уравнениях для поля отбрасываются токи смещения, т. е. полагается

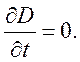
Использование гидродинамической модели означает, что мы заменяем электронную плазму заряженной жидкостью, характеризуемой несколькими параметрами:

средней плотностью, эквивалентом которой является плазменная частота ω_p;

средней скоростью носителей ;

давлением, эквивалентом которого является коэффициент диффузии Д;

средним коэффициентом трения, характеризуемым частотой рассеяния v.

6.8. Электропроводность и дрейфовые токи полупроводников
в электрических и магнитных полях

Будем рассматривать далее холодное состояние плазмы полупроводников в гидродинамическом приближении, достаточно точно описывающем поведение плазмы для многих случаев технического использования. Уравнение движения тогда будет иметь вид (86)

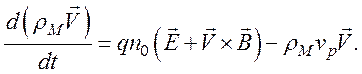
Для удобства первое слагаемое в правой части уравнения преобразуем, учитывая, что ρ_M=mn₀ – плотность жидкой частицы:

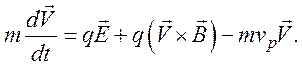                                                                                                    (87)

Далее рассмотрим поведение плазмы для некоторых важных случаев:

1. Пусть на плазму воздействует только постоянное электрическое поле , тогда (87) будет иметь вид

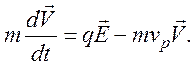                                                                                                    (88)

Поскольку поле постоянно, то и дрейфовая скорость носителей будет постоянной, т. е. 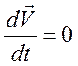 (стационарный случай). Тогда, интегрируя уравнение (88), получаем

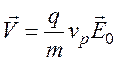
или вводя величину τ_p – среднее время свободного пробега носителей, при котором теряется средний по ансамблю частиц импульс ,

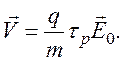
Учитывая, что электропроводность σ₀=qμN, а ток , получим

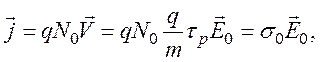
где 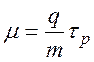 – подвижность носителей заряда в постоянном поле.

2. Пусть на плазму воздействует гармонически изменяющееся поле
 тогда из уравнения (87) получаем

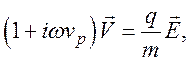
откуда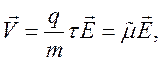                                                

где 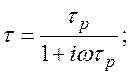                                                                                                                   (89)

 – подвижность носителей в переменном поле.

Обозначим проводимость плазмы в переменном поле как

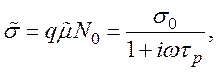
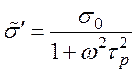 как реальную часть высокочастотной проводимости.

Для бесстолкновительного случая, когда ωτ_p>>1, из уравнения (80) с учётом уравнения (89), получим

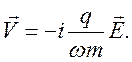
Здесь «–i» означает, что скорость носителей заряда  отстаёт по фазе относительно амплитуды электрического поля  на величину . Смещение (путь) носителей (траектория их движения) будет сдвинуто по фазе относительно поля на величину π (см. рис. 16).

Такое состояние приводит к тому, что положение вектора напряженности электрического поля  (поляризация вектора ) в плазме, обусловленная свободными носителями, оказывается противоположным положению вектора , обусловленного связанными зарядами (например диполями атомной решётки).

Поскольку именно они определяют диэлектрическую постоянную решетки, свободные носители зарядов в бесстолкновительном случае и незамагниченной плазме дают отрицательный вклад в диэлектрическую проницаемость.

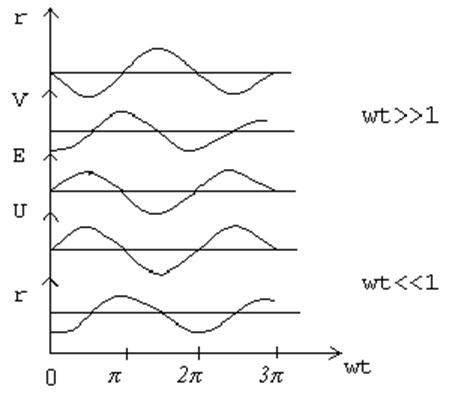
Рис. 16. Фазовые сдвиги относительно поля Е:  - скорости носителей,

– смещение по координате для положительной частицы

3. Рассмотрим поведение плазмы для случая, когда на нее действует постоянное магнитное поле, т. е.  а электрическое поле  Положим также, что v = 0, тогда уравнение движения (87) принимает вид

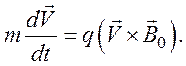
Сила , действующая на носители заряда:

 – сила Лоренца,

Сила направлена всегда ортогонально скорости движения зарядов и изменяет направление движения носителей, которые будут совершать движение по траектории, проекция которой на плоскость, перпендикулярную вектору , будет представлять окружность. Если решить уравнение движения в этой плоскости, то получим для частоты вращения носителей величину

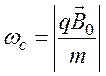 – циклотронную или Ларморовскую частоту.

Величина радиуса окружности движения частиц r_c определяется по формуле

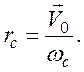
Здесь – проекция начальной скорости носителей на плоскость магнитного поля.

Для носителей заряда с безразмерной массой 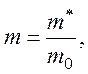 где m₀ – масса электрона в вакууме, а m^*– эффективная масса носителей заряда в полупроводнике.

,

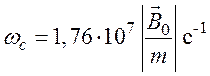где  измеряется в гауссах. При ≈10⁴гс, m = 0,1 ω_c =1,76×10¹²c^-1 .

Радиус циклотронной орбиты электронов с m^*≈0,1 при скорости
^*≈0,7 см c^-1 (тепловая скорость электронов при Т = 300 К)

r_c=1,8×10^-5 см.

Направление циклотронного вращения зависит от знака зарядов и направления магнитного поля. Если магнитное поле направлено от наблюдателя, то отрицательные частицы будут вращаться по часовой стрелке, а положительные частицы против, независимо от направления начальной скорости .