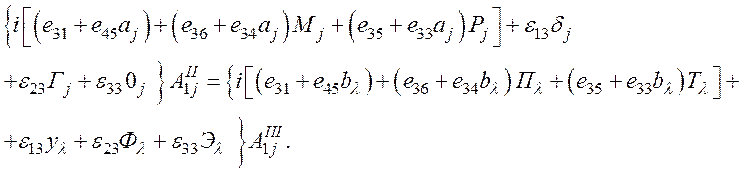 (63)
(63)
Рассмотрим граничные условия (52).
Выражения для компонент T13, T23 и T33 при условии, что x3=h, запишем в форме (31), домножив их на exp(iajkh) и получим
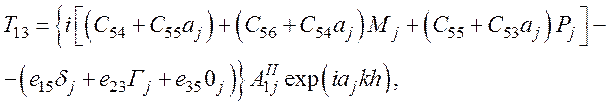 (64)
(64)
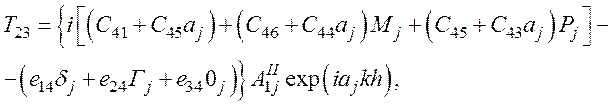 (65)
(65)
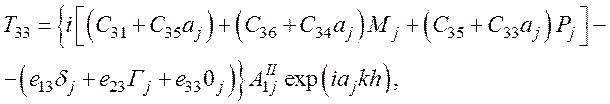 (66)
(66)
Граничные условия (53) запишем в виде следующих выражений:
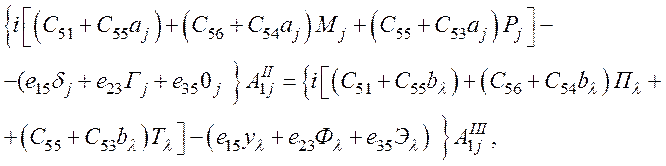 (67)
(67)
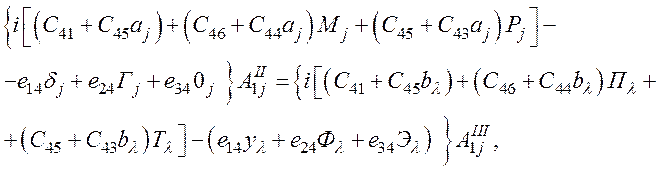 (68)
(68)
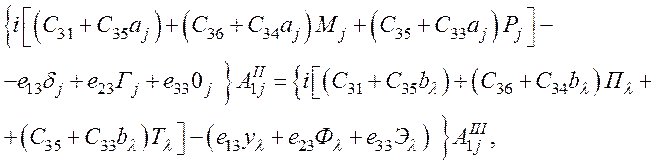 (69)
(69)
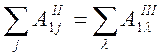 (70)
(70)
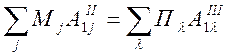 (71)
(71)
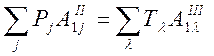 (72)
(72)
Используя соотношение (37), найдем выражение для граничных условий:
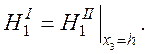
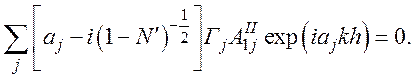 (73)
(73)
Продифференцировав выражение (35) при условии, что x3=0 получим из
граничных условий 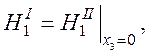
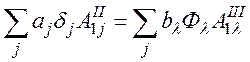 . (74)
. (74)
Сведем уравнения (60)-(74) в систему и запишем ее в матричной форме.
|
|
(75) |
![]()
Компоненты
матрицы ![]() имеют вид
имеют вид
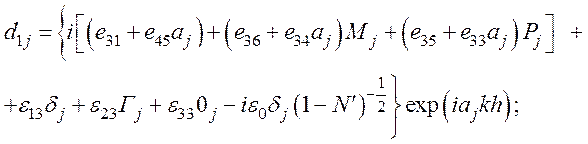
d1П=0 - из уравнения (61),
d2j=δj, d2П=-yj;
d3j=Гj, d3П=-Фλ - из уравнения (61) и (62),
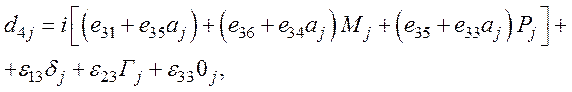
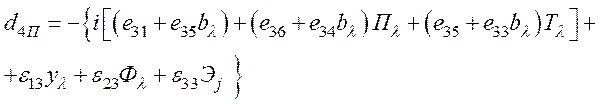
- из уравнения (63),
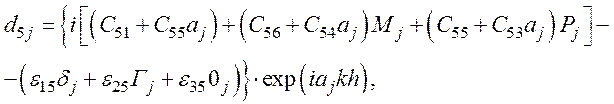
d5П=0 - из уравнения (64),
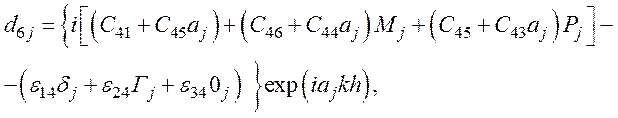
d6П=0 - из уравнения (65),
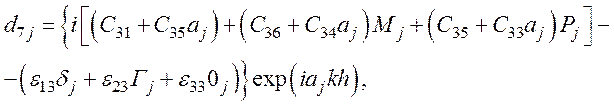
d7П=0 - из уравнения (66),
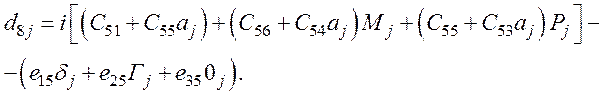
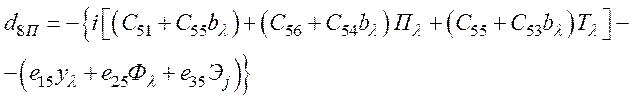
- из уравнения (67),
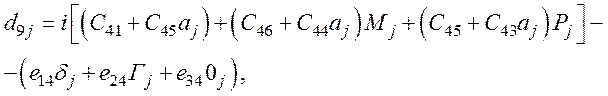
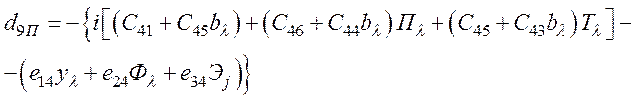
- из уравнения (68),
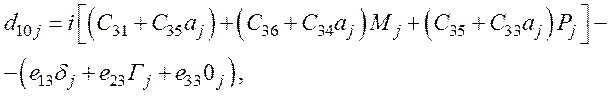
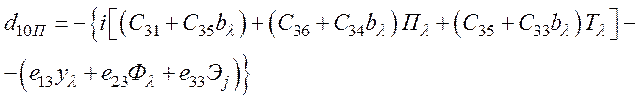
- из уравнения (69),
d11j=1, d11П=1 - из уравнения (70),
d12j=Мj, d12П=-Пλ - из уравнения (71),
d13j=Pj, d13П=-Tλ - из уравнения (72),
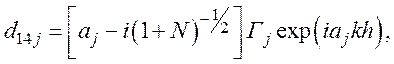
d14П=0 - из уравнения (73),
d15j=аjГj, d15П=-bλФλ - из уравнения (74).
Нетривиальным условием механических смещений и
электрических полей, ограниченных сагиттальной плоскостью, является равенство
нулю определителей |ЕГ|=0, ![]() , удовлетворяющих
граничным условиям (50)-(54), из которых должны быть исключены члены Е2=U2=0, T23=0 и Н1=0, где
, удовлетворяющих
граничным условиям (50)-(54), из которых должны быть исключены члены Е2=U2=0, T23=0 и Н1=0, где ![]() и
и ![]() будут уравнениями третьей степени
относительно a2 и b2. Поэтому для области II
существует шесть корней: j=1, 2, 3, ..., 6, а для области III
три корня и l=1, 2, 3. Тогда уравнение для граничных условий
представим в виде
будут уравнениями третьей степени
относительно a2 и b2. Поэтому для области II
существует шесть корней: j=1, 2, 3, ..., 6, а для области III
три корня и l=1, 2, 3. Тогда уравнение для граничных условий
представим в виде
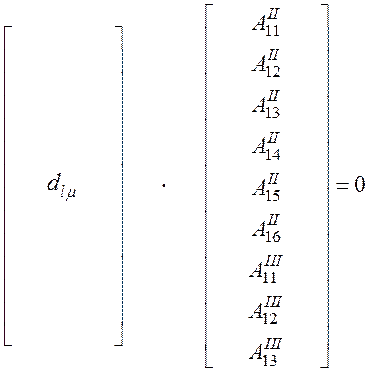
![]()
Компоненты ![]() запишем,
используя выражения для компонент dlμ трехкомпонентной
волны, исключив из них члены, относящиеся к U2, E2, T23, H1. Напомним, что j=1, 2, 3, ..., 6, n=6+l, l=1, 2, 3.
запишем,
используя выражения для компонент dlμ трехкомпонентной
волны, исключив из них члены, относящиеся к U2, E2, T23, H1. Напомним, что j=1, 2, 3, ..., 6, n=6+l, l=1, 2, 3.
Тогда
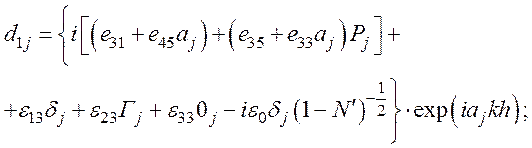
d1П=0,
d2j=δj d2П=-yλ;
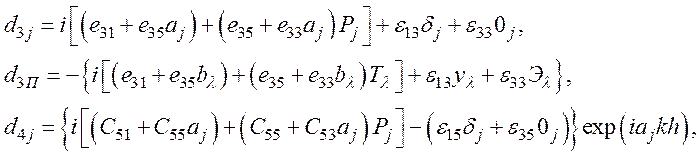
d4П=0,
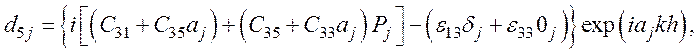
d5П=0,
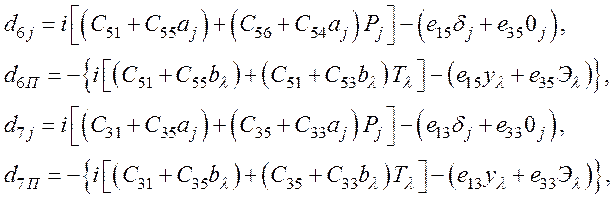
d8j=1,d8П=-1;
d9j=Pj,d8П=-Tλ.
Таким образом, детерминант dlμ для граничных условий поверхностных волн в сагиттальной плоскости для слоистой структуры имеет вид
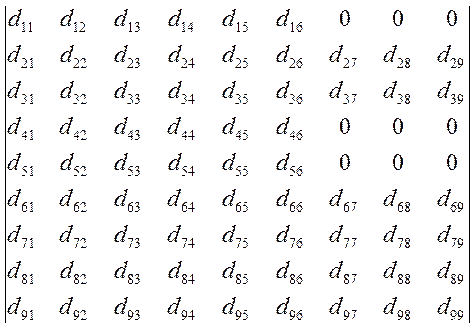
Отметим некоторые особенности поверхностных акустических волн в слоистых средах:
1. В зависимости от кристаллографической симметрии материалов слоя и подложки наблюдается сложный волновой процесс. В некоторых направлениях здесь возможно распространение различных типов волн (волны Рэлея, Лява, Стоунли и т.д.).
2. В целом волновой процесс носит многомодовый характер. Для большинства волн характерны частоты верхней либо нижней отсечки.
3. Параметры волн зависят от толщины слоя, так и от соотношения электромеханических свойств материалов слоя и подложки.
4. Волновой процесс и его параметры имеют дисперсионную зависимость.
Последние десятилетия ознаменованы бурным развитием исследований плазменных явлений в твердых телах, которые привели к возникновению новой области физики – физики плазмы твердого тела, а в последнее время и к появлению научно-технического направления функциональной микроэлектроники – плазменно-волнового.
Термин «плазма твердого тела» (ПТТ) употребляется для описания совокупности подвижных носителей заряда в твердом теле (ТТ). Такая плазма существует в металлах, полуметаллах и полупроводниках.
В металлах электронная плазма играет решающую роль в определении всех свойств кристалла. Такие важные свойства, как энергия связи, кристаллическая структура, электрические характеристики и фотонный спектр, определяются плазмоподобным поведением электронов проводимости. Поэтому для понимания свойств металлов нужно знать свойства электронной плазмы.
Плазма полупроводников и полуметаллов сильно отличается от упомянутой выше области исследований ПТТ. Эта плазма весьма разрежена по сравнению с плазмой металлов и поэтому почти не играет роли при определении общей структуры тела.
Кристалл Si, например, практически не меняется (за исключением электрических свойств) при легировании от собственной до очень высокой концентрации носителей. Поэтому изучение плазмы полупроводников не позволяет получить сведения о структуре такого кристалла, но способствует изучению большого числа других плазменных явлений.
Плазма ТТ подобна газовой плазме, однако существуют сильные количественные различия между этими двумя типами плазмы. Например, длина свободного пробега различных частиц в газовой плазме часто сравнима с ее размерами, в то время как в ПТТ это бывает редко, поэтому она является практически бесконечной средой, для которой граничные условия играют небольшую роль.
Другое отличие ПТТ от газовой плазмы связано с возможностью выведения этих систем из теплового равновесия. ПТТ представляет собой сильно связанную с решеткой однородную равновесную систему, которую можно возбудить только с помощью довольно сильного возмущения. Это обстоятельство связано с малой величиной свободного пробега электронов вследствие их взаимодействия с решеткой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.