Волновые процессы в материальных средах: Учебное пособие, страница 20

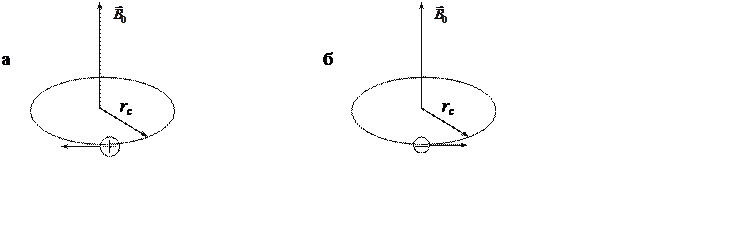
Рис. 17. Направление движения носителей зарядов: а – положительно

 заряженных носителей (дырок); б – отрицательно заряженных

 носителей (электронов)

4. Пусть на плазму одновременно воздействуют электрическое поле  и магнитное поле , причем , считаем также, что v_p = 0. Траектория движения носителей зарядов оказывается неожиданной: при включении магнитного поля носители перестают двигаться с постоянной скоростью вдоль электрического поля.

Уравнение движения (87) будет выглядеть следующим образом:

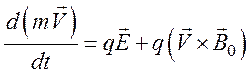                                                                                                    (90)

где                                   (91)

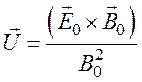
скорость поступательного движения носителей.

Используя (91), уравнение (90) преобразуем к виду

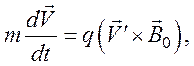                                                                                                    (92)

поскольку  

Решение (92) в случае отсутствия скорости носителей вдоль направления магнитного поля будет представлять уравнение кругового движения с постоянной скоростью  перпендикулярно электрическому и магнитному полям.

На рис. 18 показаны траектории движения носителей зарядов при =0.

rce

rcp

Ер

+

-

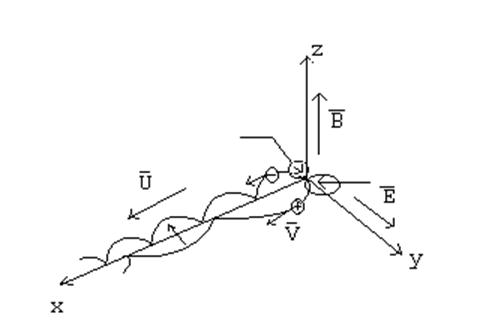
Рис. 18. Траектории движения носителей зарядов

Вследствие того что положительные и отрицательные носители зарядов в начальный момент движения перемещаются в противоположные стороны, возникает поляризация носителей зарядов, соответствующая по направлению решеточной поляризации, определяемой диэлектрическую постоянную решетки. Такая же поляризация получается и в однокомпонентной плазме, когда носители зарядов одного из знаков неподвижны.

Таким образом, в присутствии магнитного поля вклад свободных носителей в диэлектрическую проницаемость оказывается положительным, т.е. решеточная диэлектрическая проницаемость будет увеличиваться, в отличие от рассмотренного ранее случая в отсутствии магнитного поля.

Отметим так же, что если на плазму действует переменное электромагнитное поле, то и в отсутствии  будет происходить аналогичное явление, поскольку из уравнений Максвелла будет вытекать наличие магнитной компоненты, создающей силу Лоренца.

5. С учетом столкновений уравнение движения в постоянном электрическом и магнитном полях будет иметь вид

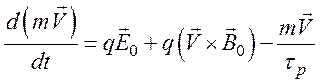                                                                                                    (93)

Пусть электрическое поле направлено по оси х₂, а магнитное поле – по оси х₃; также будем рассматривать случай стационарный, т. е. 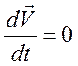. Из уравнения (93) получим

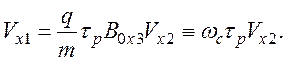                                                                                                    (94)

Таким образом, видим, что учет столкновений приводит к появлению продольного дрейфа, определяемого скоростью V_x1, наряду с поперечным со скоростью V_x2. Направление дрейфа носителей заряда составляет угол 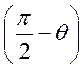 по отношению к направлению электрического поля (см. рис. 19). Если ω_cτ_p>>1, то из (94) следует

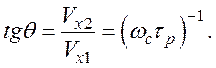
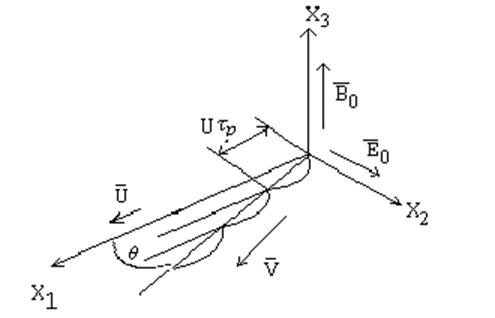
Рис. 19. Траектория движения носителей в скрещенных полях

После столкновения носители зарядов теряют свою направленную скорость  и снова начинают движение в направлении постоянного поля .

С ростом  радиус циклотронной орбиты уменьшается и носители зарядов отклоняются на меньший угол θ.

6. Пусть на плазму воздействуют  и гармоническое поле

Подставив в уравнение движения (93) значение полного поля  и значение скорости носителей зарядов, где – переменная составляющая дрейфовой скорости, получим

                                                                                                    (95)

                                                                                                    (96)

Здесь, 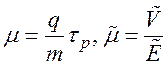 – подвижности носителей зарядов в постоянном и переменном полях.

В уравнениях (95) и (96) отброшены переменные составляющие скорости, связанные с циклотронным вращением, а также слагаемые  и . Здесь  – собственное магнитное поле электромагнитной волны, учёт которой приводит к нелинейной задаче.

Решив совместно уравнения (95) и (96), получим общее выражение для дрейфовой скорости:

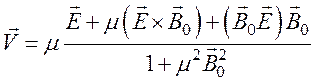                                                                                                    (97)

Подставив уравнение (97) в уравнение , можно получить выражение, определяющее ток в замагниченной плазме. Проводимость же плазмы, определяемая  для замагниченной плазмы, имеет тензорный характер:

где компоненты σ_ij имеют вид

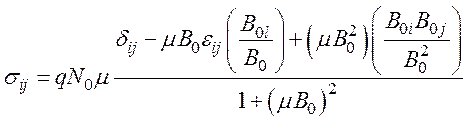                                                                                                    (98)

Когда  направлено по оси x₃, то из (98) получим

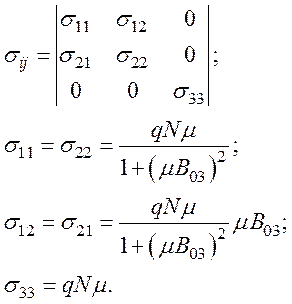
Если σ₁₂=-σ₂₁, то такие среды называются гиротропными.

В заключение отметим, что в этой главе описаны основные параметры и свойства плазмы ТТ, которые будем дальше использовать при анализе некоторых случаев распространения электромагнитных волн в этой среде.

7. Векторная запись уравнений Максвелла
 для гармонических волн

В классической электродинамике используются в основном три формы записи уравнений Максвелла: интегральная, дифференциальная и для комплексных амплитуд. Каждая из них позволяет описывать один и тот же электромагнитный процесс, но с некоторыми особенностями: интегральная форма уравнений Максвелла позволяет находить решения для полей в ограниченной условиями решения области, т. е. в ограниченном пространстве  или объёме; дифференциальная форма позволяет определять значения полей в конкретной точке пространства, заданной текущими координатами x, y, z; уравнения Максвелла для комплексных амплитуд используются для исследования гармонических процессов и позволяют исключить в уравнениях временную зависимость.

Используемые в этих формах записи символы объёмных и поверхностных интегралов, а также символы дифференциальных операторов неудобны для записи  и достаточно многообразны, поэтому в дальнейшем будем использовать другую форму уравнений Максвелла, которая отличается максимальной компактностью записи по сравнению с другими формами.