Волновые процессы в материальных средах: Учебное пособие, страница 23

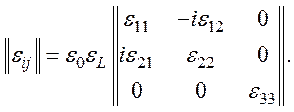
Компоненты тензора определяются следующими соотношениями:

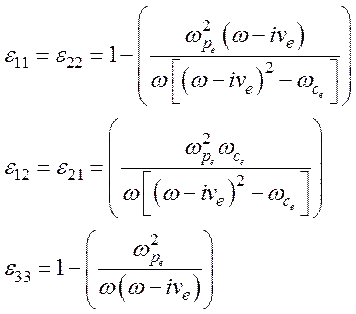
где 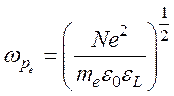 – плазменная частота электронной плазмы;

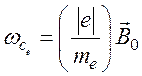 – циклотронная частота.

Поскольку плазма в магнитном поле оказывается анизотропной средой, материальное уравнение системы уравнений должно быть заменено на

D_i=ε_ijE_j,

раскрывая которое, получим

D₁=ε₀ε_L(ε₁₁E₁-iε₁₂E₂),

D₂=ε₀ε_L(ε₂₂E₂+i₁₂E₁),

D₃=ε₀ε_Lε₃₃E₃, здесь ε_L – диэлектрическая проницаемость решетки, ε₀ – диэлектрическая постоянная вакуума.

Анизотропия диэлектрических свойств плазмы вызывается силой Лоренца .

Исследование волновых мод, распространяющихся в плазме в различных полевых геометриях, будем проводить с помощью дисперсионного уравнения (109):

1.  Исследуем продольные электрокинетические волны или волны пространственного заряда (рис.20).

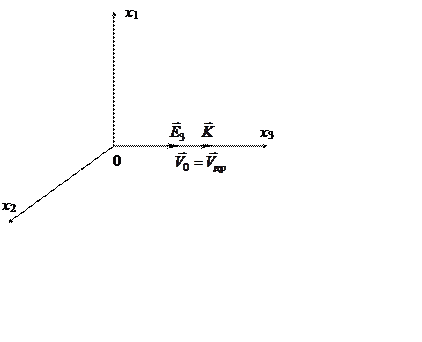
Рис. 20. Геометрия исследуемого случая распространения волн

Продольную компоненту поля E₃ будем искать в уравнении вида

Здесь и далее символ «~» означает переменную величину первого порядка малости.

Решив совместно уравнения (1) и (3) системы уравнений (103) и (118), получим

Уравнение (3) системы (103) преобразуется к виду

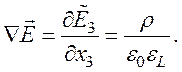
Уравнение (3) системы (118) преобразуется к виду

                                                                                                  (119)

Уравнение (1) системы (118) преобразуется к виду

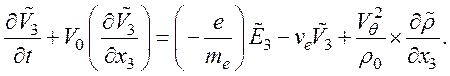                                                                                                  (120)

Далее рассмотрим эти уравнения для следующих значений величин:

В этом случае (имеются столкновения носителей и диффузия).

Решая совместно уравнения (119), (120), получаем дисперсионное уравнение

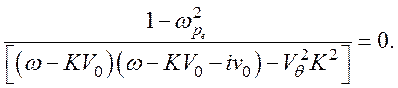                                                                                                  (121)

Выражения для  имеют вид

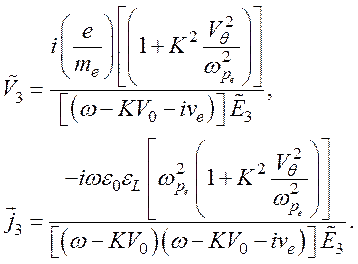
Дисперсионное уравнение (121) имеет следующее решение:

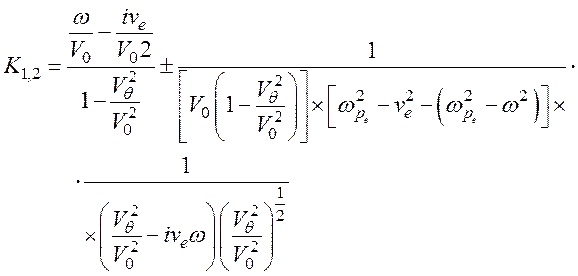                                                                                                 (121а)

т. е. дисперсионное уравнение имеет два решения, соответствующих волновым числам K₁ и K₂. Иначе говоря, для одной и той же частоты ω существуют две моды с волновыми числами K₁ и K₂.

Рассмотрим поведение и характеристики этих мод.

1. Пусть V_θ=0, v_e=0, т. е. столкновения отсутствуют, дрейф носителей тоже. Тогда

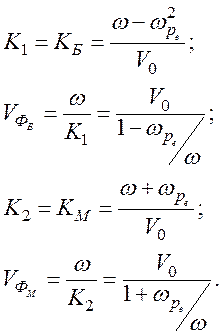
Таким образом, этому случаю соответствуют две волны. Одна быстрая со скоростью , а другая медленная со скоростью .

2. Если V_θ=0, v_e≠0, то

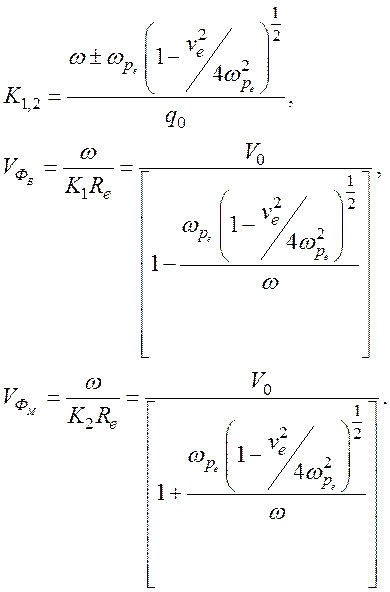
Видим, что столкновения приводят к затуханию волн, определяемых мнимыми частями волновых векторов

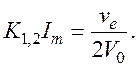
3. Если V_θ=0, т. е. частота столкновений значительна, но диффузии носителей еще нет, то

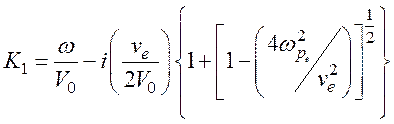                                                                                                  (122)

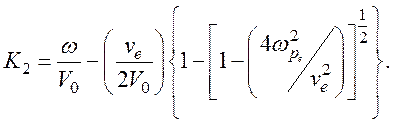                                                                                                  (123)

Как видно из уравнения (122) и (123), обе волны имеют одинаковые волновые числа, а значит, и одинаковую фазовую скорость, равную дрейфовой скорости носителей

Этот случай определяет так называемые синхронные волны.

4. Если V_θ=0,  то

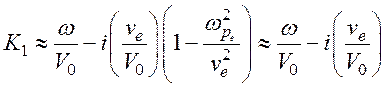
или

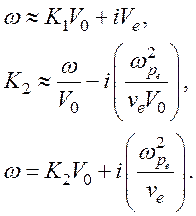                                                                                                  (124)

Мода с волновым числом K₁ оказывается сильно затухающей.

В электронном потоке с преобладающими столкновениями остается только одна мода с K₂, определяемым уравнением (124).

5. Пусть  V_θ≠0 и 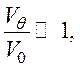 тогда

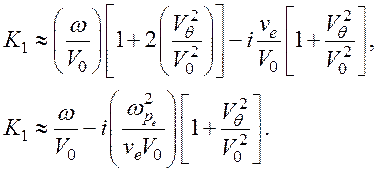
В случае преобладающих столкновений и наличия диффузии увеличиваются потери для обеих мод, а фазовая скорость сильно затухающей моды уменьшается до значения, определяемого по формуле

.

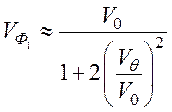Таким образом, в присутствии тянущего электрического поля в плазме возможно возбуждение и распространение продольных электрокинетических волн, быстрых и медленных по отношению к дрейфовой скорости носителей заряда V₀.

Эти волны – волны плотности носителей, или волны объемного заряда отрицательного в области избыточной концентрации электронов и положительного в области нескомпенсированого заряда доноров, сопровождаются переменным электрическим полем.

Параметры волн будут определяться величиной полей E₃, концентрацией носителей n₀, диэлектрическими свойствами конкретных полупроводниковых материалов и их состояния.

2. Далее исследуем поперечные электрокинетические волны.

Рассмотрим случай, полевая геометрия которого представлена на рис. 21.

На неограниченную плазму в направлении оси x₃ одновременно воздействуют электрическое поле  и магнитное поле .

В соответствии с формулой рассмотрим волну с правой поляризацией  которая вращается в том же направлении, что и электроны в магнитном поле. Волна с левой поляризацией  будет вращаться в направлении, противоположном направлению вращения электронов в магнитном поле.

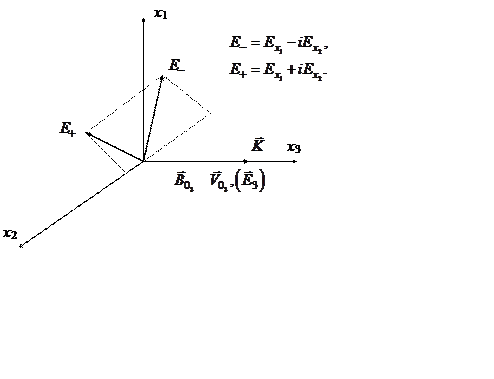
Рис. 21. Полевая геометрия волны

Волновое уравнение (105) должно быть дополнено уравнением движения (1) системы уравнений (118), в котором отбросим последнее слагаемое (рассматриваем холодную плазму): т. е.

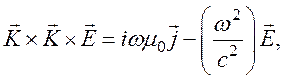                                                                                                  (125)

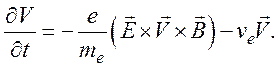
Из формулы находим

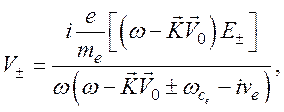
а ток

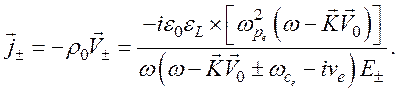                                                                                                  (126)

Совместное решение уравнений (125) и (126) приводит к уравнению

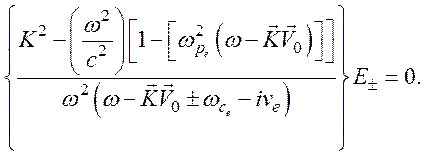
Из которого получаем дисперсионное уравнение

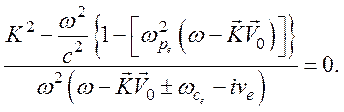
Это квадратное относительно волнового вектора уравнение имеет два решения K₁ и K₂, которым соответствуют две моды поперечных волн: электромагнитная быстрая, определяемая K₁, и электрокинетическая медленная, определяемая волновым вектором K₂.

Волна, определяемая волновым вектором K₂, имеет малое затухание и называется геликоновой.

9. энергия электрокинетических волн

9.1. Теорема Пойнтинга для слабого сигнала
продольных электрокинетических волн

Электрокинетические волны с энергетической точки зрения бывают с положительной и отрицательной энергией.

Для возбуждения волны с положительной энергией к системе нужно добавить энергию высокочастотного поля, т.е. средняя энергия потока носителей e₀ должна увеличиться e₀+De, а для возбуждения волны с отрицательной энергией (медленной волны) энергия потока носителей e₀-De.