Таблица 5
|
Поляризация |
Напряжение |
|||||
|
s1 |
s2 |
s3 |
s4 |
s5 |
s6 |
|
|
p1 |
Lэф |
Tэф |
Tэф |
Ls |
Ts |
Ts |
|
p2 |
Tэф |
Lэф |
Tэф |
Ts |
Ls |
Ts |
|
p3 |
Tэф |
Tэф |
Lэф |
Ts |
Ts |
Ls |
Lэф, Tэф, Ls, Ts ![]() − коэффициенты пьезоэлектрических
эффектов. Коэффициенты Tэф, Lэф.определяют
электрическую поляризацию, вызванную напряжениями сжатия или растяжения, а
коэффициенты Ls, Ts −
поляризацию, вызванную напряжениями сдвига (рис. 5).
− коэффициенты пьезоэлектрических
эффектов. Коэффициенты Tэф, Lэф.определяют
электрическую поляризацию, вызванную напряжениями сжатия или растяжения, а
коэффициенты Ls, Ts −
поляризацию, вызванную напряжениями сдвига (рис. 5).
Коэффициенты Lэф, т. е. пьезомодули d11, d22, d33, определяют связь между растягивающим (или сжимающим) напряжением и поляризацией в том же направлении.
В поперечных эффектах Tэф − поляризация, перпендикулярная вызывающей ее деформации растяжения (сжатия) и определяемая пьезомодулями d12, d13, d23, d32, d31, d21.
Эффекты типа Ls − это эффекты продольного сдвига: поляризация параллельна оси сдвига и нормальна по отношению к плоскости сдвига. Сюда относятся пьезомодули d14, d25, d36. Наконец, эффекты типа Ts − это эффекты поперечного сдвига: сдвиговое напряжение вызывает поляризацию в плоскости сдвига, поперечную к оси сдвига; связь между вектором поляризации и сдвиговым напряжением определяется пьезомодулями d15, d16.
Физический смысл и численная величина компонент пьезомодуля зависят от принятого расположения осей.

Рис. 5. Пьезоэлектрический эффект
Электрическая поляризация кристаллов при прямом пьезоэффекте может быть вызвана не только приложенным механическим напряжением sij, согласно (11), но и механической деформацией Uij кристалла:
pi=eijkUjk. (12)
Пьезоэффект можно характеризовать поляризацией ![]() или напряженностью
или напряженностью ![]() электрического поля возникших
зарядов:
электрического поля возникших
зарядов:
Ei=gijk×sjk, (13)
Ei=hijk×Ujk (14)
Пьезоэлектрические коэффициенты e, h, g также составляют тензоры 3-го ранга. Матрицы коэффициентов g не отличаются от d, а для h и e есть отличия в нескольких классах.
Коэффициенты g, e, h, g взаимно связаны, их можно выразить друг через друга и использовать для характеристики определенных эффектов или приборов.
Если электризация кристалла при механическом воздействии, т. е. прямой пьезоэлектрический эффект, описывается уравнением
pi=dijksjk,
то обратный пьезоэлектрический эффект, т. е. изменение формы кристалла под действием приложенного электрического поля, подчиняется уравнению
Uij=dijkEk.
Механическое напряжение и электрическая поляризация при прямом пьезоэффекте связаны теми же коэффициентами, что и электрическое поле, и механическая деформация при обратном эффекте. Такие обратные соотношения справедливы и для уравнений (12), (13), (14).
Пьезоэлектрические кристаллы − эффективные электромеханические преобразователи. Они могут преобразовывать механическую энергию в электрическую вследствие прямого пьезоэлектрического эффекта, или электрическую энергию в механическую вследствие обратного эффекта.
Соотношение между подводимой и получаемой энергиями определяет меру эффективности электромеханического преобразователя и характеризуемую коэффициентом электромеханической связи
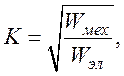
где
Wмех![]() − механическая энергия упругих
деформаций колеблющегося пьезоэлектрического кристалла; Wэл− электрическая
энергия.
− механическая энергия упругих
деформаций колеблющегося пьезоэлектрического кристалла; Wэл− электрическая
энергия.
Для случая преобразования k-й компоненты электрического поля ij -й компонентой механической деформации коэффициент
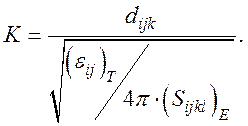
Здесь ![]() − компонента
диэлектрической проницаемости, измеренная при постоянной температуре;
− компонента
диэлектрической проницаемости, измеренная при постоянной температуре; ![]() − компонента тензора упругой жесткости,
измеренная при постоянном электрическом поле.
− компонента тензора упругой жесткости,
измеренная при постоянном электрическом поле.
Коэффициент K не является тензорной величиной, но он зависит от тензорных величин, т. е. не одинаков для разных направлений в кристалле.
Н а п р я ж е н и я. Механическим напряжением называется сила, действующая на единицу площади. Будем рассматривать лишь такие напряженные состояния твердых тел, при которых напряжения во всем теле однородны, все части тела находятся в состоянии статического равновесия, объемные силы и объемные моменты равны нулю.
Выделим внутри напряженного тела единичный куб с ребрами, параллельными осям x1, x2, x3. Все силы, действующие на этот куб, можно разложить на компоненты, действующие на его грани (рис. 6).
Введем следующие обозначения:
sij− компонента силы, действующей в направлении оси xi, например s12 есть компонента силы, действующей в направлении оси x1 на площадку, нормальную к оси x2.
Компоненты s11, s22, s33 являются нормальными (т. е. растягивающими или сжимающими), s12, s21, s13, s31, s23, s32 − сдвиговыми, лежащими в плоскости тех площадок, на которые они действуют.
Растягивающее напряжение считают положительным, сжимающее − отрицательным.
Таким образом, в общем случае напряженное состояние тела определяется системой из девяти компонент: три нормальных и шесть сдвиговых.
В теории упругости доказано, что эти девять компонент образуют тензор 2-го ранга − тензор механических напряжений:

Рис. 6. Ориентация компонент тензора механических напряжений
Вследствие условий однородности напряжения и статического равновесия нормальные и сдвиговые компоненты не создают моментов на гранях, к которым они приложены, а следовательно,
s12=s21, s13=s31, s23=s32, или sij=sji.
Тензор механических напряжений является симметричным тензором и приводится к главным осям. Если направления главных осей выбраны за оси координат, то сдвиговые компоненты напряжения равны нулю, а тензор имеет вид
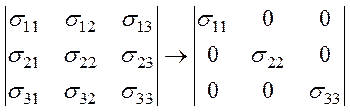
В дальнейшем обозначим их так:
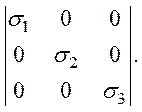
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.