Волновые процессы в материальных средах: Учебное пособие, страница 7

Диэлектрик состоит из частиц двух типов отрицательных А и положительных В ионов. Структура диэлектрика такова, что кристаллическая решетка имеет центр симметрии. Если диэлектрик поместить в электрическое поле, то в результате перемещения ионов толщина пластины изменится (увеличится) и станет равной x₂ (рис. 3). Очевидно, что изменение знака поля не вызовет изменения знака деформации и также приведет к увеличению толщины образца. При этом x₂ = x₃. Это явление, характеризующееся деформацией диэлектрика при приложении к нему электрического поля и не зависящее от знака поля, называется электрострикцией.

Электрострикция является четным эффектом. В первом приближении величина деформации Sпропорциональна квадрату электрического поля:

S=RE²,

где R − коэффициент электрострикции, являющийся в общем случае тензором 4-го ранга; S_ij=R_ijklE_k×E_l.

Электрострикция наблюдается у всех диэлектриков: твердых, жидких, газообразных. Однако коэффициент электрострикции для линейных диэлектриков очень мал (~10^-12 ед). При сжатии или растяжении кристалла материальные заряженные частицы изменяют свое положение, поэтому изменяется величина элементарного дипольного момента, образованного зарядами разных знаков. Однако изменения поляризации диэлектрика не произойдет, так как при центросимметричном расположении зарядов изменению электрического момента будет соответствовать равное по величине изменение электрического момента отрицательного диполя, в результате чего суммарный эффект будет равен нулю. Таким образом, у кристалла, обладающего центром симметрии, эффекта, обратного электрострикции, не наблюдается.

Совершенно иначе будет вести себя кристалл, у которого нет центра симметрии в распределении зарядов (рис. 4).

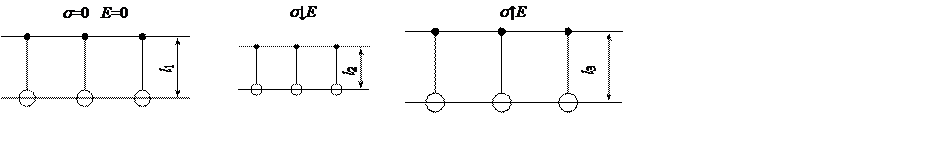
Рис. 4. Положение зарядов, не имеющих центра симметрии

в электрическом поле

При воздействии на такой кристалл механического напряжения сжатия  элементарный момент будет уменьшаться (l₂<l₁), а при действии растягивающего механического усилия дипольный момент будет увеличиваться (l₃>l₁). Это приведет к изменению поляризации кристалла или плотности заряда на его поверхности. Эффект, при котором изменяется электрический момент кристалла при воздействии на него механического напряжения, называется прямым пьезоэлектрическим эффектом. Зависимость между изменением поляризации или плотности заряда на поверхности кристалла и механическим напряжением в одномерном случае определяется в первом приближении уравнением

                                                                                                           (10)

где  − физическая константа, называемая пьезоэлектрическим модулем.

Из (10) следует, что изменение знака s (замена сжатия растяжением) приводит к изменению знака .

При пьезоэлектрическом эффекте возникшее в кристаллах электрическое поле можно охарактеризовать вектором электрической поляризации , вектором электростатической индукции  или вектором , а действующее на кристалле механическое усилие − тензором механических напряжений s_ik или тензором деформаций U_ij. Таким образом, тензорное воздействие вызывает векторное явление (или обратно): p_i→s_ik. Следовательно, связывающее их свойство кристалла должно быть тензором 3-го ранга.

В общем случае (пока без учета влияния симметрии кристалла) каждая компонента вектора p связана с каждой компонентой тензора s соотношением

p_i=d_i11s₁₁+d_i12s₁₂+d_i13s₁₃+d_i21s₂₁+d_i22s₂₂+d_i23s₂₃+d_i31s₃₁+d_i32s₃₂+d_i33s₃₃

или

p_i=d_ijks_jk.                                                                                                    (11)

Входящие в эти уравнения 27 компонент образуют тензор 3-го ранга − так называемый тензор пьезоэлектрических модулей d_ijk.

Из-за симметрии тензора механических напряжений s_jk его компоненты
s_jk =s_kj, а число независимых компонент тензора d_ijk можно сократить до 18.

Для записи компонент тензора d_ijk применяют сокращенные матричные обозначения, которые вводятся так:

11	22	33	23,32	31,13	12,21
↓	↓	↓	↓	↓	↓
1	2	3	4	5	6

В этой записи компоненты тензора напряжений T_ij принимают вид

s₁₁→s₁, s₂₂→s₂, s₃₃→s₃, s₂₃→s₄,

s₃₁=s₁₃→s₅, s₁₂=s₂₁→s₆.

Аналогично можно представить компоненты тензора любого ранга.

В тензоре пьезоэлектрических модулей d_ijk запишем следующее:

d_i11→d_i1, d_i22→d_i2, d_i33→d_i3,

а для компонент d_ijk=d_ikj примем обозначения

2d_i11=d_i4, 2d_i31=d_i5, 2d_i12=d_i6.

Например,

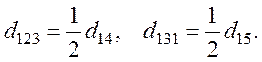
В сокращенных матричных обозначениях уравнение (11) записывается так:

p_i=d_i1s₁+d_i2s₂+d_i3s₃+d_i6s₆+d_i5s₅+d_i4s₄

или в общем виде:  p_m=d_mn×s_n,

где  m=1, 2, 3,  n=1, 2,…,6.

Матричные обозначения компактнее тензорных, но следует помнить, что они не преобразуются как компоненты тензора. Для того чтобы проводить тензорные преобразования, нужно сначала перейти от сокращенной, матричной записи к тензорной. Представим матрицу пьезомодулей в новом сокращенном виде:

	s1	s2	s3	s4	s5	s6
p1	d11	d12	d13	d14	d15	d16
p2	d21	d22	d23	d24	d25	d26
p3	d31	d32	d33	d34	d35	d36

Как определить физический смысл каждой из этих компонент, например, как расшифровать, что такое d₁₄? Для этого перейдем от сокращенной записи к полной:

d₁₄=d₁₃₂+d₁₂₃  , т. е. p₁=(d₁₂₃+d₁₃₂)s₂₃.

Если в кристалле коэффициент d₁₄¹0, значит, под действием сдвигового напряжения, приложенного в направлении оси x₂ к площадке, нормальной к оси x₃ (или в направлении x₃ к площадке, нормальной к оси x₂), возникает электрическая поляризация, определяемая составляющей вектора P₁, направленной вдоль оси x₁. Таков смысл пьезомодуля d₁₄.

Анализируя таким способом все 18 пьезомодулей, видим, что они определяют четыре типа пьезоэлектрических эффектов (см. табл. 5).

Четыре типа пьезоэлектрических эффектов