1.
Пусть Vq=0, а 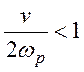 . Тогда мода К1 –
быстрая волна, т.к. Vф1>V0, другая
мода К2 – медленная волна, т.е. Vф2<V0
. Тогда мода К1 –
быстрая волна, т.к. Vф1>V0, другая
мода К2 – медленная волна, т.е. Vф2<V0
при 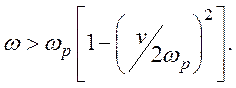
2.
Vq=0, а 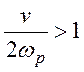 , то Vф1=Vф2=V0, т.е.
волны находятся в синхронизме с дрейфовым движением. Следовательно,
действительная часть потока электрокинетической энергии положительна для
быстрой волны и отрицательна для медленной при условии достаточно редких
столкновений: v<2wp. При v>2wp обе волны имеют
одинаковую фазовую скорость, равную V0, и действительную часть потока электрокинетической
энергии, равную нулю, т.е.
, то Vф1=Vф2=V0, т.е.
волны находятся в синхронизме с дрейфовым движением. Следовательно,
действительная часть потока электрокинетической энергии положительна для
быстрой волны и отрицательна для медленной при условии достаточно редких
столкновений: v<2wp. При v>2wp обе волны имеют
одинаковую фазовую скорость, равную V0, и действительную часть потока электрокинетической
энергии, равную нулю, т.е.
![]()
Рассмотрим плотность энергии для потока носителей с учетом столкновений и диффузии. Из уравнения (137) следует, что
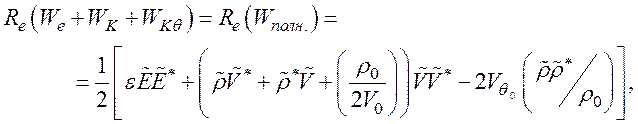 (140)
(140)
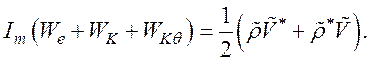 (141)
(141)
Здесь ![]() определяется
формулой (138),
определяется
формулой (138), ![]() определим из уравнения непрерывности
как
определим из уравнения непрерывности
как 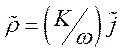 , а
, а ![]() из
формулы (139). Таким образом, уравнения (140) и (141) представим в виде
из
формулы (139). Таким образом, уравнения (140) и (141) представим в виде
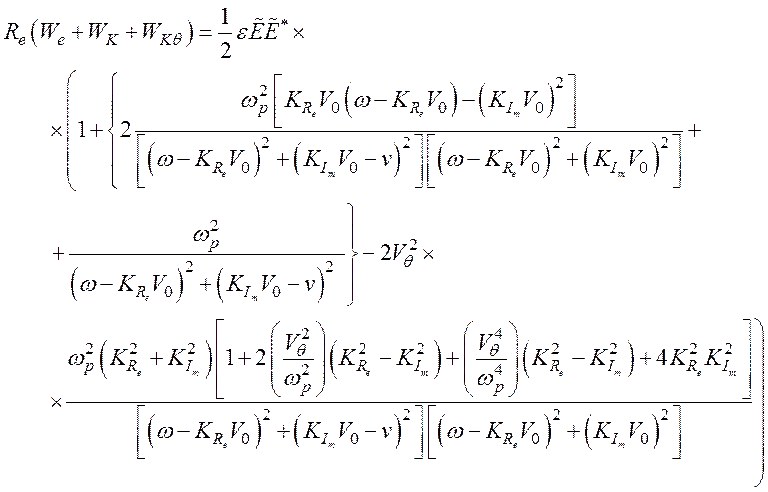 (142)
(142)
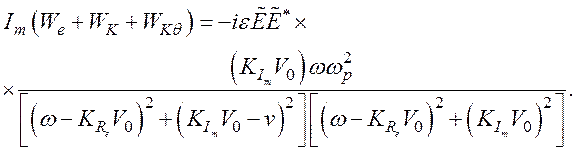 (143)
(143)
В уравнении (142) первый член в правой части представляет действительную часть плотности электромагнитной энергии We. Для чисто продольной моды эта плотность энергии является чисто электрической. Второй и третий члены представляют действительную часть плотности электрокинетической энергии WK. Последний член – это плотность тепловой энергии WKq.
Рассмотрим влияние столкновений и диффузии на примере нескольких предельных случаев.
1. Из уравнения (121а) получаем моды холодной бесстолкновительной плазмы, для которой Vq=0, v=0:
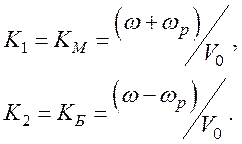
Тогда WKq=0 и Wполн.=Wе+ WK, а
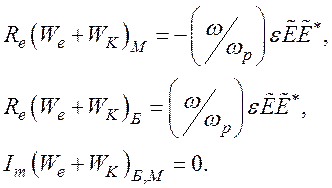
Здесь плотность энергии отрицательна для медленной волны и положительна для быстрой волны, а
(РК)М,Б=V0(Wполн.)М,Б.
2. Если v>>2wp, а VД=0,
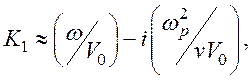 (144)
(144)
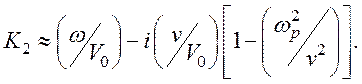 (145)
(145)
Vф1=Vф2=V0 – синхронны обе моды.
Мода, соответствующая К2, сильно затухающая уже при w<<v, и ею можно пренебречь.
Подставив (144) и (145) в (142) и (143), получим
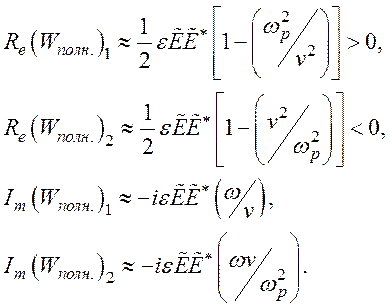
Действительная часть полной плотности энергии для
слабозатухающей моды К1, положительна. Большая часть энергии
запасается в поле 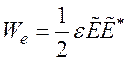 .
.
Электрокинетическая часть 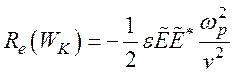 отрицательна
и мала. Для сильнозатухающей моды К2 большая часть энергии
заключена в электрокинетической форме
отрицательна
и мала. Для сильнозатухающей моды К2 большая часть энергии
заключена в электрокинетической форме
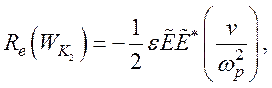
и эта величина большая. Действительные части плотности электрокинетической энергии отрицательны для обеих мод из-за потерь энергии вследствие столкновений.
3. v>>2wр, w, v>>KV0 – частые столкновения Vq¹0, Vq<< V0.
Слабозатухающая мода
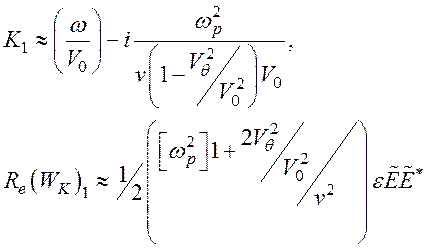 (146)
(146)
- действительная часть электрокинетической энергии.
Уравнения (146) показывают, что диффузия увеличивает потери.
Среды,
содержащие свободные носители и не спаренные локализованные электроны, которые
являются причиной намагничивания, в макроскопическом отношении характеризуются
тензорами диэлектрической и магнитной проницаемости 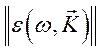 и
и
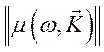 или соответствующими тензорами
восприимчивости
или соответствующими тензорами
восприимчивости 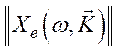 и
и 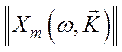 .
Материальные уравнения тогда имеют вид
.
Материальные уравнения тогда имеют вид
![]() (147)
(147)
![]() (148)
(148)
где ![]() и
и ![]() -
векторы электрической и магнитной поляризации,
-
векторы электрической и магнитной поляризации,
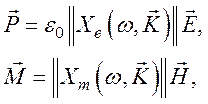
Подставляя их в (147) и (148), получаем
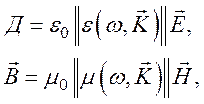
где
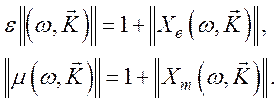
Уравнения Максвелла тогда будут иметь вид
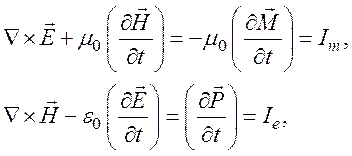
где
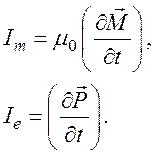
Теорема Пойнтинга в этом случае имеет вид
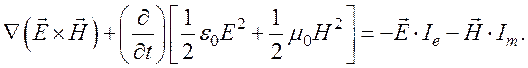
Если применить преобразование Фурье по времени и
пространству, то зависимости будут гармоническими вида expst, где S=v+iw, и вида ![]() , где
, где ![]() .
.
Представим далее плотности токов намагничивания и электрической поляризации в виде
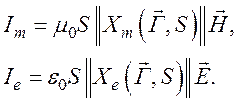
В стационарном состоянии S=iw, поэтому зависимость компонент Фурье от времени будет содержать
множитель exp(iwt),
а тензорные величины восприимчивости можно представить как 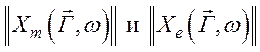 . Получим среднее по времени
действительные величины в стационарном состоянии, записав теорему Пойнтинга для комплексных полей:
. Получим среднее по времени
действительные величины в стационарном состоянии, записав теорему Пойнтинга для комплексных полей:
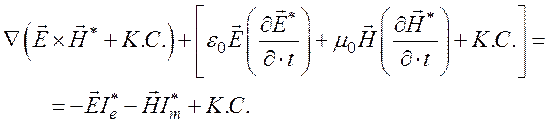 (149)
(149)
Для стационарного состояния с зависимостью от iwt
пространства
-![]() соотношение (149) преобразуется к
виду
соотношение (149) преобразуется к
виду
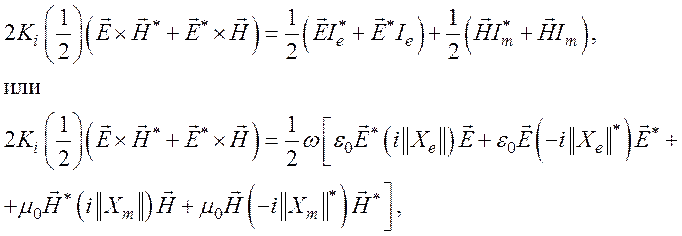
или сокращенно
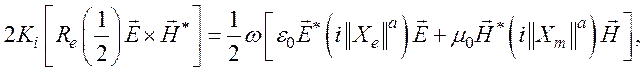
где ![]() и
и ![]() - антиэрмитовы части от
- антиэрмитовы части от![]() и
и ![]() .
.
Для пассивной среды с потерями выражения ![]() и
и ![]() положительно
определены.
положительно
определены.
Если ![]() и
и ![]() есть отрицательно определенные
величины, то среда будет активной, т.е. будет генерироваться средняя по времени
электромагнитная мощность.
есть отрицательно определенные
величины, то среда будет активной, т.е. будет генерироваться средняя по времени
электромагнитная мощность.
Если же эти величины будут равны нулю, то среда будет без потерь.
Рассмотрим далее среду с малыми потерями, или
слабоактивную среду, т.е. такую, у которой ![]() .
Поля, как и прежде, зависят от времени гармонически expst, S=v+iw и r<<w.
.
Поля, как и прежде, зависят от времени гармонически expst, S=v+iw и r<<w.
Уравнение Максвелла тогда можно записать в виде
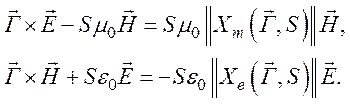
Теорема Пойнтинга для комплексных полей (149) преобразуется к виду
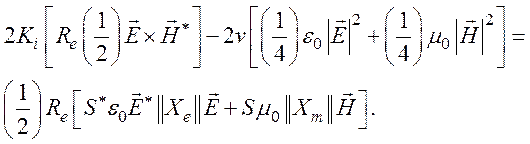 (150)
(150)
Разложим ![]() в ряд Тейлора на
члены первого порядка, т.к. будем полагать, что v<<w и
в ряд Тейлора на
члены первого порядка, т.к. будем полагать, что v<<w и ![]() :
:
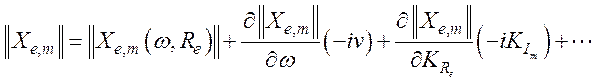 (151)
(151)
Из уравнений (150) и (151) находим
![]()
Здесь 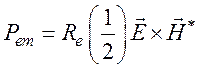 - средний по
времени поток электромагнитной энергии;
- средний по
времени поток электромагнитной энергии;
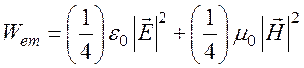 - средняя по
времени плотность электромагнитной энергии.
- средняя по
времени плотность электромагнитной энергии.
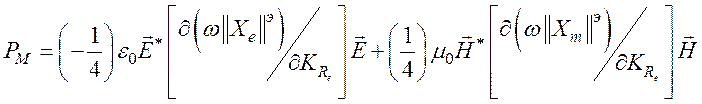 - средний по
времени поток из-за поляризации среды;
- средний по
времени поток из-за поляризации среды;
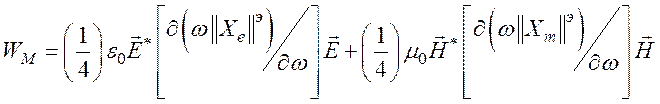 - средняя по времени
плотность энергии поляризуемой среды;
- средняя по времени
плотность энергии поляризуемой среды;
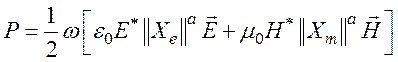 - средняя
мощность потерь.
- средняя
мощность потерь.
Применим полученные результаты к анализу продольных и поперечных электрокинетических волн.
Пренебрегая потерями (ve=0, Vq=0), получаем для продольных и поперечных электрокинетических волн
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.