Поверхностные пьезоэлектрические волны в слоистых тонкопленочных средах широко применяются в электроакустических устройствах. Используя материалы первой главы, проведем общий анализ и получим основные соотношения для волн, распространяющихся в слоистых тонкопленочных средах (рис. 14).

Рис. 14. Схема исследуемой структуры
Систему уравнений, которой должен подчинятся волновой процесс, представим в следующем виде:
для области I:
![]() , (41)
, (41)
для области II (слоя)
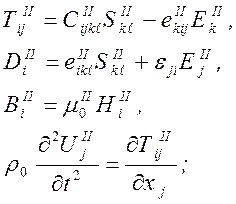 (42)
(42)
для области III:
во всех выражениях (42) следует произвести замену индексов II на III.
В каждой области должны также удовлетворяться уравнения Максвелла:
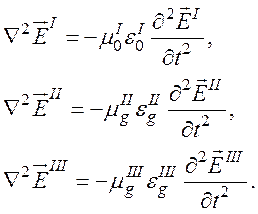 (43)
(43)
Рассмотрим плоские поверхностные волны, распространяющиеся в направлении оси x1, с экспоненциально затухающей амплитудой в направлении оси x3. Смещение и компоненты напряженности электрического поля запишем в виде:
для области I:
![]() (44)
(44)
для области II:
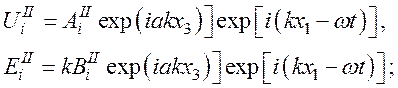 (45)
(45)
для области III:
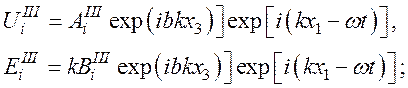 (46)
(46)
После преобразований, аналогичных сделанных в гл. 1, получим характеристические уравнения:
где
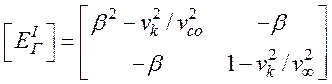 (47)
(47)
и
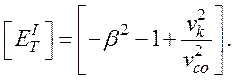
Для области II и III возможны три формы характеристических уравнений, соответствующие типам волн, которые могут распространятся в среде в данном направлении:
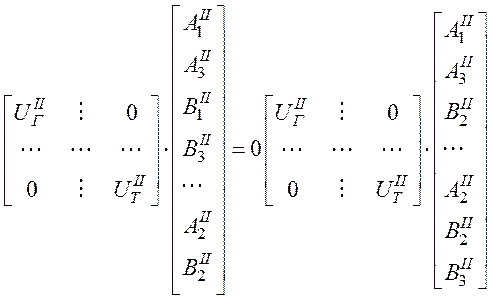 (48)
(48)
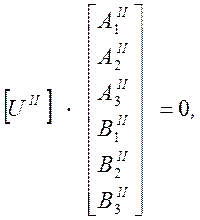 (49)
(49)
где UII
соответствует выражению (21); ![]() и
и ![]() - частные случаи от UII.
- частные случаи от UII.
Для области III в выражениях (48) следует заменить индекс II на III.
Уравнение (48), как видно, может иметь две различные
формы. Первая из них определяется равенством нулю коэффициентов ![]() и определителей
и определителей ![]() и
и ![]() и
соответствует волне Рэлея и Сезава в слоистых системах.
и
соответствует волне Рэлея и Сезава в слоистых системах.
Нулевые значения коэффициентов ![]() ,
,
![]() и определителей
и определителей ![]() и
и ![]() соответствуют
нулевым механическим смещениям и электрическим полям, перпендикулярным направлению
распространения, и определяют диапазон волн Лява.
соответствуют
нулевым механическим смещениям и электрическим полям, перпендикулярным направлению
распространения, и определяют диапазон волн Лява.
Случай, соответствующий равенству нуля только
определителей ![]() (49) соответствует сложной
трехкомпонентной поверхностной волне.
(49) соответствует сложной
трехкомпонентной поверхностной волне.
Электрические поля поверхностных волн в общем случае должны удовлетворять граничным условиям, таким, что касательные компоненты электрического поля, компонента электрического смещения, нормальная к поверхности, и продольная компонента магнитного поля должны быть непрерывны у границ областей:
У x3=h
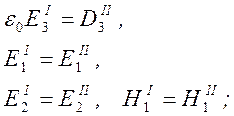 (50)
(50)
У x3=0
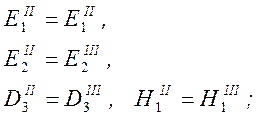 (51)
(51)
Упругие граничные условия требуют, чтобы компоненты напряжений T13, T23, T33, исчезали на свободной поверхности и были непрерывными на границе областей II и III. Кроме того, должны быть непрерывными и механические смещения Ui:
при x3=h: ![]() (52)
(52)
при x3=0: ![]() (53)
(53)
![]() (54)
(54)
Общими условиями существования такой волны является условие (49), т.е. |UII|=|UIII|=0, и граничные условия (50)-(54).
Используя (36) для |UII| и |UIII|, запишем характеристическое уравнение рассматриваемого случая поверхностных волн.
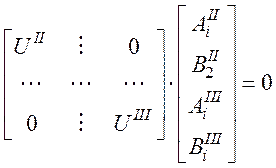 (39)
(39)
Для получения нетривиального решения этого уравнения, потребуем равенства нулю его определителя |U|=0. Определитель |U| является ступенчатым и равен произведению его диагональных клеток: |U|=|UII|·|UIII|.
Выражения |UII| и |UIII| в общем виде являются уравнениями пятой степени относительно a2 и b2. Тогда выражения электрических полей и механических смещений запишем в форме (56):
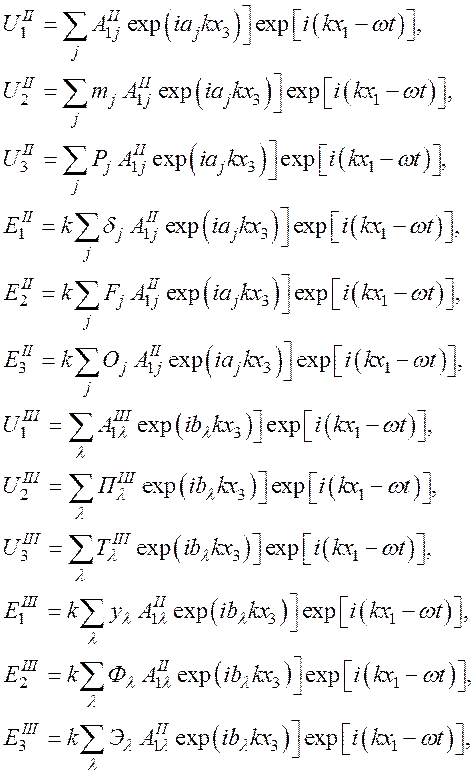 (56)
(56)
где i=1, 2, …, 10; l=1, 2, …, 5.
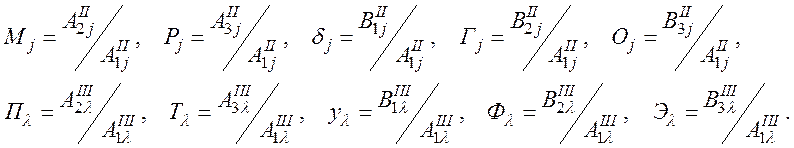
Обратимся к граничным условиям (50) – (54).
Подставив выражение ![]() из
(44),
из
(44), ![]() и
и ![]() из
(56) и
из
(56) и ![]() из (42) в (50) и, учитывая значение x3=h, получим
из (42) в (50) и, учитывая значение x3=h, получим
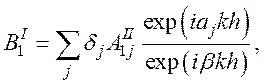 (57)
(57)
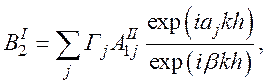 (58)
(58)
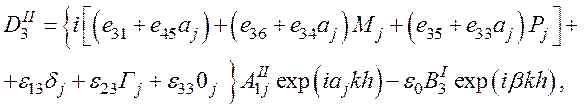 (59)
(59)
Подставив
в (59) значение ![]() из (30) и учитывая
из (30) и учитывая ![]() в форме (57), получим
в форме (57), получим
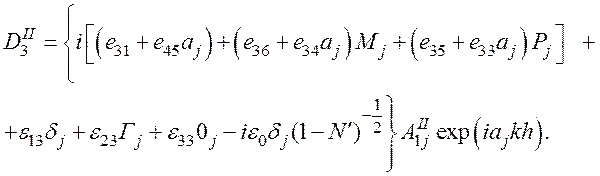 (60)
(60)
Рассмотрим граничные условия (51). Подставив выражения для компонент напряженности электрического поля из (56) в (51) и учитывая значение x3=0, имеем
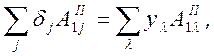 (61)
(61)
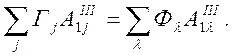 (62)
(62)
Выражения для ![]() и
и
![]() запишем из (59), исключив из них
член
запишем из (59), исключив из них
член ![]() . Далее сделаем соответствующую
замену обозначений амплитудных коэффициентов и констант затухания для области III.
Сократив слева и справа множители exp(iajkh) и exp(ibλkh), получим
. Далее сделаем соответствующую
замену обозначений амплитудных коэффициентов и констант затухания для области III.
Сократив слева и справа множители exp(iajkh) и exp(ibλkh), получим
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.