На квантово-механическом языке возбуждение волны с положительной энергией означает рождение когерентных плазмонов, или когерентных (коррелированных) электрон-дырочных пар, при поглощении когерентных продольных фотонов. Возбуждение волны с отрицательной энергией означает уничтожение когерентных электрон-дырочных пар при испускании когерентных продольных фотонов, или когерентных плазмонов.
Итак, если энергия высокочастотного поля передается потоку носителей, т.е. поток действует как положительная резистивная нагрузка для поля, то возбуждение электрокинетическая потоковая мода с положительной энергией. Полная энергия потока eполн. Будет равна сумме энергии постоянной составляющей движения потока e0 и высокочастотной энергии De, переданной от волны.
Если же высокочастотное поле отбирает энергию от потока, т.е. поток действует как отрицательная резистивная нагрузка для волны, то возбуждена электрокинетическая потоковая мода с отрицательной энергией. Полная энергия потока будет равна разности энергий постоянной составляющей энергии движения потока и высокочастотной энергии, передаваемой от потока к волне, т.е.
eполн=e0-De.
Уравнения Максвелла линейно связывают поля Е и Н с их источниками:
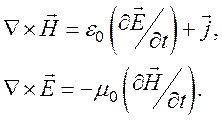
Для периодических процессов по времени все величины можно разложить в ряд Фурье. Первые гармоники поля должны удовлетворять уравнениям
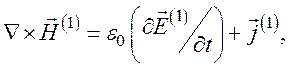 (127)
(127)
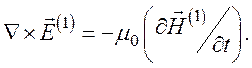 (128)
(128)
Теорема Пойнтинга для первых гармоник получается при использовании тождества
![]()
и уравнения (127) и (128):
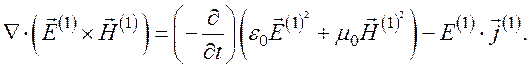 (129)
(129)
Интегрируя уравнение (129) по фиксированному объему V,
окруженному стационарной поверхностью 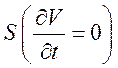 ,
получаем
,
получаем
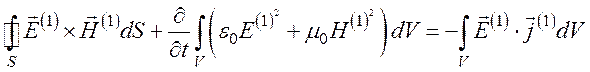
Первый член в левой части равенства представляет электромагнитную мощность, заключенную в полях с частотой основной гармоники и вытекающую из объема через граничную поверхность.
Второе слагаемое в левой части – это скорость изменения электромагнитной энергии, связанной с этими полями. Правая часть – это мощность, теряемая или выделяемая в элементе объема на основной частоте вследствие присутствия свободных носителей.
Если перейти к пределу слабых сигналов, то поля
гармоники с основной частотой Е(1) и Н(1)
становятся совпадающими с линеаризованными полями ![]() ,
член
,
член ![]() обычно представляют в виде суммы
дивергенции потока электрокинетической мощности и скорости изменения плотности
энергии.
обычно представляют в виде суммы
дивергенции потока электрокинетической мощности и скорости изменения плотности
энергии.
Таким образом, уравнение (129) можем записать в следующем виде:
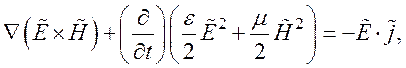 (130)
(130)
где e =e0eL, m=m0 (среда предполагается немагнитной и проводящей).
Из уравнения (130) видно, что электромагнитная энергия
и мощность не сохраняются в присутствии носителей. Энергия, теряемая или
приобретаемая в единице объема за единицу времени, равна ![]() . Получим выражение, определяющее
член
. Получим выражение, определяющее
член ![]() через электрокинетические
переменные.
через электрокинетические
переменные.
Линеаризованное уравнение движения для одномерного потока имеет вид
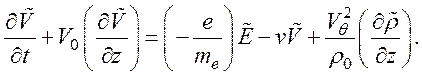 (131)
(131)
Здесь V0 – скорость дрейфа в направлении оси z.
Из (131) получим
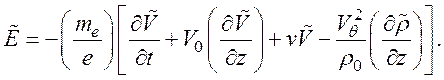 (132)
(132)
Переменная составляющая тока слабого сигнала в одномерном случае будет равна
![]() (133)
(133)
Решая совместно уравнения (132) и (133), получаем
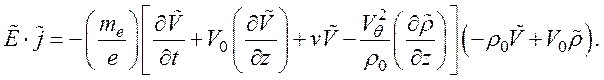 (134)
(134)
С учетом уравнения (1) системы уравнений ( ) и уравнения непрерывности, уравнение (134) запишем в виде
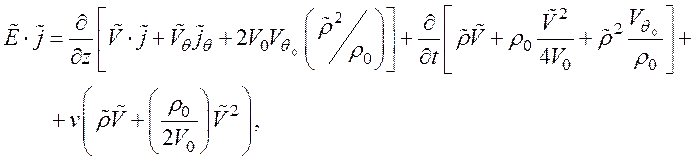 (135)
(135)
где 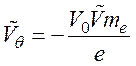 - переменный
электрокинетический потенциал;
- переменный
электрокинетический потенциал;
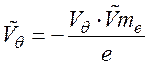 - переменная
составляющая электрокинетического потенциала, образующаяся вследствие диффузии;
- переменная
составляющая электрокинетического потенциала, образующаяся вследствие диффузии;
![]() - - переменная составляющая плотности
тока, связанного с диффузией;
- - переменная составляющая плотности
тока, связанного с диффузией; 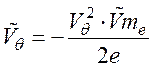 - постоянная
составляющая теплового или диффузионного потенциала.
- постоянная
составляющая теплового или диффузионного потенциала.
Решая совместно уравнения (130) и (135), получаем линеаризованную форму теоремы Пойнтинга с учетом эффектов столкновений и диффузии:
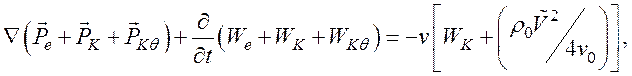 (136)
(136)
где ![]() - поток
электромагнитной энергии через единичную площадку;
- поток
электромагнитной энергии через единичную площадку;
![]() - поток электрокинетической
энергии через единичную площадку;
- поток электрокинетической
энергии через единичную площадку;
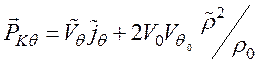 - поток тепловой
энергии через единичную площадку;
- поток тепловой
энергии через единичную площадку;
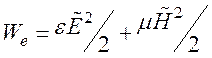 - плотность
электромагнитной энергии;
- плотность
электромагнитной энергии;
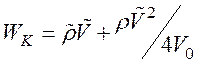 - плотность
электрокинетической энергии;
- плотность
электрокинетической энергии;
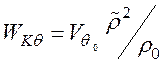 - плотность
тепловой энергии.
- плотность
тепловой энергии.
Для комплексных переменных величин перепишем уравнение (136) в виде
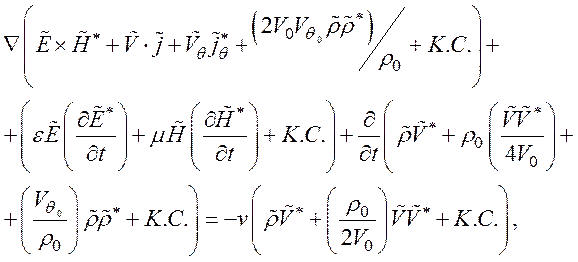
где К.С. означает комплексно-сопряженные величины.
Далее учтем, что зависимость всех переменных величин и все члены с производными по времени будут равны нулю:
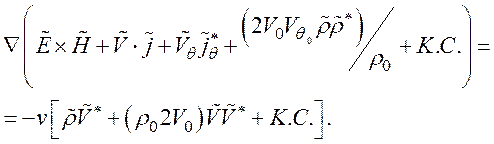 (137)
(137)
Далее рассматриваем действительную часть потока электрокинетической энергии:
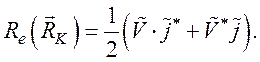
Из уравнения (131) и уравнения Пуассона найдем выражение для электрокинетического потенциала:
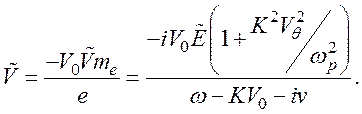 (138)
(138)
Из уравнения непрерывности запишем переменную плотности тока:
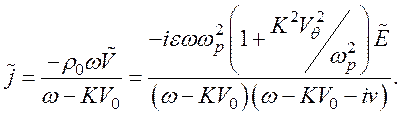 (139)
(139)
Диффузия увеличивает влияние переменного электрического поля на величину
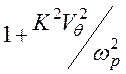 .
.
Таким образом,
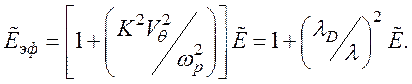
Диффузия (тепловые эффекты) приводит к появлению потока тепловой энергии РКq и плотности тепловой энергии WКq и увеличивает поток и плотность электрокинетической энергии. Поэтому часть тепловой энергии и мощности в системе заключена в электрокинетической форме.
Если Д=0, при ![]() получим
получим
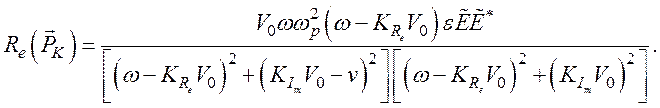
Знак ![]() зависит от знака
множителя
зависит от знака
множителя ![]() . Поскольку
. Поскольку 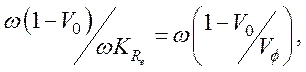 то
этот знак зависит от относительной величины дрейфовой скорости потока V0 и фазовой скорости
то
этот знак зависит от относительной величины дрейфовой скорости потока V0 и фазовой скорости 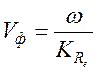 волны, поддерживаемой потоком.
волны, поддерживаемой потоком.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.