Поляризация этих трех волн, распространяющихся с разными скоростями, всегда взаимно перпендикулярны. Векторы потока энергии, определяющие направление переноса энергии для каждой из этих волн, образуют разные углы с волновыми векторами. Такие волны не представляют интереса на практике. Для устройств в этом случае приходится выбирать особые направления в кристаллах, такие, как оси симметрии, вдоль которых распространяются чистые моды. У них вектор потока энергии и волновой вектор параллельны как в изотропном твердом теле.
На поверхности бесконечной среды может распространяться сложная волна – волна Рэлея. В случае изотропного твердого тела эта волна содержит продольную и поперечную компоненты, сдвинутые по фазе на π/2 и лежащие в сагиттальной плоскости, определенной волновым вектором и нормалью к поверхности (рис. 10).
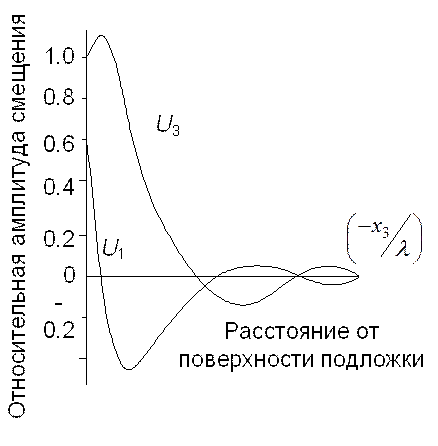
Рис. 10. Волна Рэлея
Каждая из компонент убывает с ростом глубины по-разному. Поскольку продольная компонента меняет знак, проходя через нуль на глубине, примерно равной 0,2l, поляризация волны становится чисто поперечной, а затем эллиптической с противоположным направлением вращения. Смещение частиц становится равным нулю на глубине порядка 2l (рис. 11).
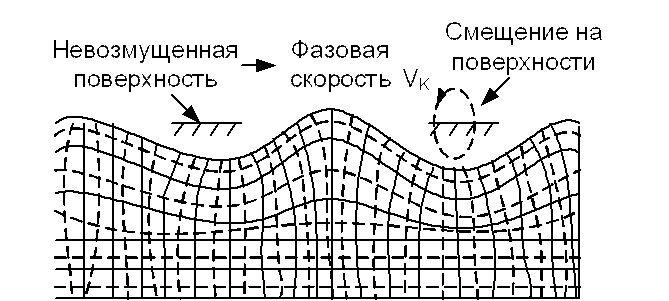
Рис. 11. Колебания частицы в волне Рэлея
На поверхности пьезоэлектрической среды возможно распространение поперечной поверхностной волны, поляризованной параллельно поверхности (рис. 12), с глубиной проникновения тем меньше, чем сильнее пьезоэлектрические свойства среды. Толщина слоя вещества, находящегося в движении под действием этих волн, называемых волнами Гуляева – Блюстейна, больше, чем в случае волн Рэлея, и может составить около 100 l[1].
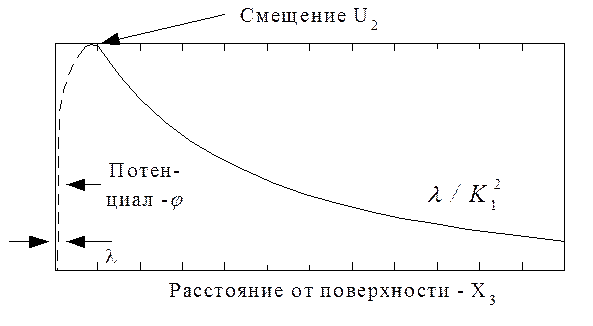
Рис. 12. Волна Гуляева – Блюстейна
Поверхностные
упругие волны, распространяющиеся вдоль поверхности полубесконечного
пьезоэлектрика, в общем случае могут иметь три компоненты механического
смещения ![]() и три компоненты электрического поля
и три компоненты электрического поля
![]() .
.
При определенных условиях, зависящих от симметрии кристаллов, эта общая форма поверхностных волн разделяется на две простые формы. Такие условия встречаются, когда распространение волны не зависит от поперечной координаты и существует в особых направлениях кристаллов некоторых классов симметрии.
Математически это разложение возможно, когда
уравнения, регулирующие механические смещения и электрические поля, сокращаются
до двух независимых наборов уравнений. В одном наборе имеются две компоненты механических
смещений ![]() , поперечное смещение
, поперечное смещение ![]() и некоторые компоненты
электрического поля. Математически, в безразмерной форме, их можно представить
в виде:
и некоторые компоненты
электрического поля. Математически, в безразмерной форме, их можно представить
в виде:
Случай
1: 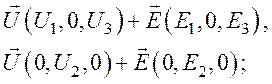
Случай
2: 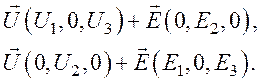
Согласно принятой классификации различают:
1. Рэлеевскую пьезоэлектрическую поверхностную волну:
![]()
2. Упругую Рэлеевскую волну:
![]()
3. Электрическую волну Гуляева – Блюстейна:
![]()
4. Поперечную поверхностную волну:
![]()
Рассмотрим распространение упругой пьезоэлектрической волны вдоль поверхности полубесконечного тела, ограниченного плоскостью х3 = 0. Ось х3 будем считать направленной перпендикулярно поверхности (рис. 13).
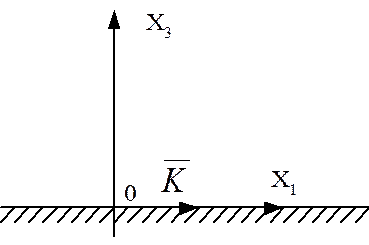
Рис. 13. Система координат
Система уравнений, которой должен подчиняться волновой процесс, состоит из уравнений упругости, уравнений состояния пьезоэлектрика и уравнений Максвелла:
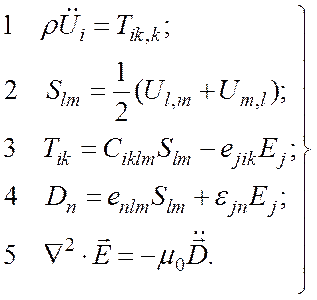 (17)
(17)
Здесь
![]() – уравнение движения;
– уравнение движения; 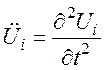 – ускорение частицы твердого тела,
участвующей в колебательном движении;
– ускорение частицы твердого тела,
участвующей в колебательном движении; 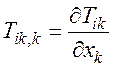 –
сила, действующая на единичный объем.
–
сила, действующая на единичный объем.
Ускорение 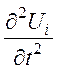 вдоль оси i,
сообщаемое этой силой массе r единичного объема
определяется из уравнения
вдоль оси i,
сообщаемое этой силой массе r единичного объема
определяется из уравнения
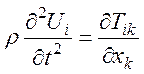 .
.
Первое уравнение системы (17), таким образом, является уравнением движения
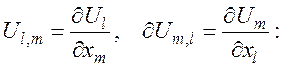
Уравнение два системы (17) есть тензор деформаций.
Уравнения два и три – уравнения состояния пьезоэлектрических кристаллов для тензора механических напряжений Тik и электрической индукции Dn.
Член уравнения три CiklmSlm выражает закон Гука, а ejikEj – пьезоэлектрическую добавку к компонентам тензора механических напряжений за счет обратного пьезоэлектрического эффекта, а всё уравнение представляет обобщенный закон Гука для пьезоэлектрических кристаллов.
Член уравнения четыре enlmSlm обозначает добавку к вектору электрической индукции за счет прямого пьезоэлектрического эффекта. Оператор Лапласа:
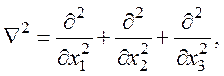
Тik, Slm, Ciklm – компоненты тензоров соответственно напряжений, деформаций и упругих модулей; εjn – компоненты тензора диэлектрической проницаемости; eijk – компоненты тензора пьезоэлектрической постоянной; ρ – плотность среды; Ej, Dn – компоненты вектора напряженности электрического поля и электрической индукции, пятое уравнение системы (17) – есть волновое уравнение Гельмгольца, m0 - магнитная постоянная вакуума.
Компоненты механических смещений и напряженности электрического поля представлены в виде:
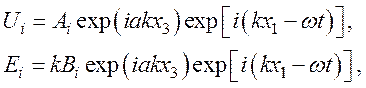 (18)
(18)
где Ai, Bi – константы; i=1, 2, 3; к – волновое число; a – произвольная постоянная затухания в направлении оси x3.
Предполагаемое решение соответствует поверхностной волне в том случае, если величина a в каждом члене решения такова, что амплитуды всех компонент смещения стремятся к нулю при x3→-∞.
Подстановка (18) в (17) приводит к системе однородных уравнений относительно Ai и Bi.
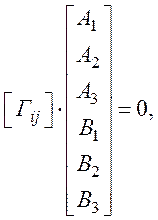 (19)
(19)
где [Гij] записывается в форме (20).
Для получения нетривиального решения этой системы потребуем равенства нулю детерминанта системы (19)
[Гij] = 0. (21)
Это приведет к уравнению пятой степени относительно a2. Корни этого уравнения, лежащие в верхней комплексной полуплоскости, соответствуют волнам вида (18), неограниченно нарастающим при x3→-∞. В задаче о распространении поверхностных волн эти решения нужно отбросить.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.