Волновые процессы в материальных средах: Учебное пособие, страница 6

Если тензор 4-го ранга симметричен по обеим парам индексов, то он имеет 36 независимых компонент. В тензорной записи изображается в развернутом виде таблицей (9х9), а при переходе к матричной записи − таблицей (6х6), т. е. вместо 81 содержит только 36 компонент.

Для тензоров выше 2-го ранга при переходе от тензорной к матричной записи (и наоборот) в ряде случаев требуется при приравнивании по правилу (9) соответствующих компонент вводить дополнительные численные множители (2, 4 и т. п.).

Использование для симметричных тензоров матричных обозначений приводит к резкому сокращению записи. Поэтому такой способ выражения очень удобен при решении многих конкретных задач, а также при использовании в кристаллофизике аппарата матричного исчисления.

Для преобразования компонент тензора по правилам (из табл. 3) при переходе от одной системы координат к другой необходимо вернуться от матричных обозначений к тензорам.

2.9. Материальные и полевые тензоры

Тензоры в зависимости от их отношения к объекту бывают двух видов: тензоры, описывающие свойства кристалла, т. е. соотношения между измеримыми величинами (материальные тензоры), и тензоры, описывающие воздействия на кристалл и его реакцию (полевые тензоры).

Симметрия материальных тензоров согласуется с симметрией кристалла. Симметрия полевых тензоров не связана с симметрией кристалла, поэтому они могут иметь любую ориентацию по отношению к элементам симметрии кристалла.

Например, можно к кристаллу любой симметрии приложить как угодно ориентированное электрическое поле (полярный вектор) или механическое напряжение (симметричный полярный тензор 2-го ранга).

Одни и те же физические тензоры в различных случаях могут выступать то в качестве материальных, то в качестве полевых. Так, вектор поляризации   обычно является полевым тензором, однако у пироэлектриков и сегнетоэлектриков вектор  описывает свойство спонтанной поляризации и согласуется с симметрией кристалла. Тензор деформации, обычно являющийся полевым, становится материальным и согласуется с симметрией кристалла, когда описывает спонтанную деформацию сегнетоэлектриков.

2.10. Кристаллофизические системы координат

Характерной особенностью физических свойств кристаллов является их анизотропия и симметрия. Вследствие периодичности, закономерности и симметрии внутреннего строения в кристаллах обнаруживается ряд свойств, которые невозможны в изотропных телах.

Анизотропные физические свойства кристаллов чрезвычайно чувствительны к влиянию внешних воздействий. Поэтому, подбирая и комбинируя эти воздействия, можно вызывать в кристаллах уникальные свойства для различных устройств в области микроэлектроники.

Для описания физических свойств кристаллов пользуются правой прямоугольной системой координат (кристаллофизической системой координат), определенным образом ориентированной относительно кристаллографических осей.

Для кубической, тетрагональной и ромбической сингоний оси кристаллофизической системы координат x₁, x₂, x₃ совпадают с кристаллографическими x, y, z. Для остальных сингоний кристаллофизические оси ориентированы относительно кристаллографических по правилам стандартной установки (см. табл. 4).

Однако при решении многих технических задач удобнее использовать не кристаллофизическую систему координат. Это необходимо, когда используются пластины кристаллов, сложно ориентированные относительно кристаллографических или кристаллофизических систем координат, когда те или иные физические свойства наиболее сильно проявляются в этих направлениях.

Таблица 4

Ориентация кристаллофизической системы координат

с кристаллографическими направлениями

Сингония	x1	x2	x3
Триклинная	В плоскости, перпендикулярной направлению [001]	[010]	[001]
Моноклинная	В плоскости (100)	[010]	[001]
Ромбическая	[100]	[010]	[001]
Тетрагональная	[100]	[010]	[001]
Тригональная и гексагональная	[2110]	[0110]	[0001]
Кубическая	[100]	[010]	[001]

3. ФИЗИЧЕСКИЕ  СВОЙСТВА  КРИСТАЛЛОВ

3.1. Пьезоэлектрический эффект

Пьезоэлектрический эффект состоит в том, что под действием механического напряжения или деформации в кристалле возникает электрическая поляризация, величина и знак которой зависят от приложенного напряжения.

Обратный пьезоэлектрический эффект − это механическая деформация кристалла, вызываемая приложенным электрическим полем, причем величина и тип деформации зависят от величины и знака поля.

Диэлектрик, помещенный в электрическое поле, поляризуется. При этом происходит изменение вектора поляризации , который определяется как суммарный дипольный момент единицы объема диэлектрика:

.

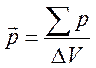Здесь Sp − суммарный электрический момент частиц (атомов, молекул, ионов), находящихся в объеме DV; , где l − расстояние между центрами тяжести образующих диполь положительного и отрицательного зарядов q.

Это изменение поляризации происходит за счет изменения положений электрических зарядов в объеме диэлектрика. Так как каждый заряд связан с элементарной частицей, молекулой или некоторым молекулярным комплексом, то изменение положения заряда приводит к изменению размеров образца диэлектрика. Характер связи деформации с электрическим полем и количественная сторона этой зависимости определяются структурой диэлектрика.

Рассмотрим тонкую пластинку диэлектрика толщиной x₁. Упрощенная двухмерная электрическая структура этого диэлектрика представлена на
рис. 3.

Рис. 3. Положения зарядов, имеющих центр симметрии в электрическом поле:
○ − отрицательный ион; ● − положительный ион