Волновые процессы в материальных средах: Учебное пособие, страница 5

Наименование	Ранг тензора	Закон преобразования
		новых компонент через старые	старых компонент через новые
Скаляр	0	j¢=j	j¢=j
Вектор	1
Тензор	2
Тензор	3
Тензор	4

Законы преобразования тензоров являются фундаментальными и служат для наиболее строгого определения понятия тензора.

Если в произвольной системе координат девять коэффициентов T_ij линейно связывают компоненты векторов p_i и q_i и при переходе от одной системы координат к другой T_ij преобразуются согласно (4) и (5), то они образуют тензор второго ранга.

В общем случае тензор ранга Nимеет Nиндексов, каждый из которых (в трехмерном пространстве) может принимать значения от 1 до 3. Поэтому тензор ранга Nимеет 3^N компонент, т. е. тензор 2-го ранга имеет 9 компонент (3), а тензор 3-го ранга имеет 27 компонент (3).

Таким образом, тензором ранга rназывается совокупность 3^rсоставляющих, имеющих r индексов, которые при изменении системы координат преобразуются последующему закону:

T¢_…ijk…=…a_ila_jma_kn…T…_lmn.

Подобно тому, как тензор 2-го ранга связывает два вектора, тензор 3-го ранга связывает вектор и тензор 2-го ранга, т. е.

a_i=T_ijkQ_jk.

Тензор 4-го ранга может связывать два тензора 2-го ранга, т. е.

R_ij=T_ijklQ_kl,

или вектор и тензор 3-го ранга:

a_i=T_ijR_ijkl.

Если тензор ранга N выражает связь между тензорами рангов L и M, то
L +M = N Тензоры можно рассматривать и как результат дифференцирования тензоров по тензорам. Так, тензором 2-го ранга будет производная вектора по вектору или вторая производная скаляра по векторным аргументам, т. е.

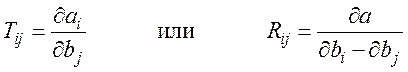
Можно показать, что они преобразуются согласно уравнениям преобразования и являются тензорами 2-го ранга.

2.7. Симметричные и антисимметричные тензоры.
Внутренняя симметрия тензоров

Тензоры обладают свойствами симметрии по отношению к своим индексам.

Если компоненты тензора не изменяются при перестановке двух или более индексов, то тензор называется симметричным относительно этих индексов.

Если  T_ij=T_ji,

T_ijk=T_ikj,                                                                                                      (6)

T_ijkl=T_klij,

то тензоры симметричны. Примером симметричного тензора является следующий тензор:

D

Обозначим это свойство как T_ij

D

Тензор T_ijk симметричен относительно двух последних индексов, т. е. T_ijk

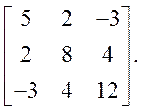
Например, симметричны следующие компоненты: T₁₁₃=T₁₃₁.

Тензор T_ijkl симметричен относительно перестановки первой и второй пар индексов и относительно перестановки индексов в парах, что можно обозначить следующим образом: T_ijkl

Выполнение условий (6) приводит к тому, что в тензоре уменьшается число независимых компонент. Симметричный тензор 2-го ранга будет иметь из 9 компонент только 6 независимых, т. е.

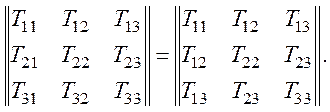
а у тензора 3-го ранга независимыми будут только 18.

Симметричность тензора ранга N по паре индексов дает 3^N-1 соотношений между его компонентами и уменьшает число независимых компонент до 3^N - 3^N-1 = 2×3^N-1

Симметричность тензора ранга N по двум парам индексов дает 5×3^N-2 соотношений между его компонентами и уменьшает число независимых компонент до 3^N - 5×3^N-2 = 4×3^N-2

Если компоненты тензора остаются неизменными при четном числе перестановок индексов и изменяют свой знак при нечетном числе перестановок, то тензор называется антисимметричным (кососимметричным) относительно этих индексов.

Если T_ij=−T_ij,

T_ijk=−T_ijk,                                                                                                           (7)

то тензор T_ij антисимметричен, а тензор T_ijk антисимметричен относительно 2-го и 3-го индексов.

Для тензора T_ij это означает, что

T₁₁=T₂₂=T₃₃=0.

Например, 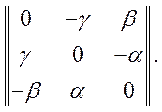                                                                                                           (8)

Выполнение условий (7), как видно, не только уменьшает число независимых компонент антисимметричного тензора, но некоторые компоненты здесь обращаются в нуль. В антисимметричном тензоре 2-го ранга, как это видно из (8), имеются всего три независимых компоненты. Можно показать также и то, что тензор остается симметричным или антисимметричным и при переходе к новой системе координат, т. е. свойство симметричности и антисимметричности тензора относительно некоторых индексов или группы индексов является инвариантом ортогонального преобразования. Это свойство характеризует внутреннюю симметрию тензоров.

2.8. Матричные обозначения

Для симметричных (полностью или по нескольким индексам) тензоров, вследствие уменьшенного числа независимых компонент, можно использовать не тензорные, а более краткие матричные обозначения с уменьшенным числом индексов, что делает запись уравнений более компактной.

Так, два индекса симметричного тензора 2-го ранга, пробегающие значения от 1 до 3, можно заменить одним индексом, пробегающим значения от 1 до 6. Связь между индексами при этом следующая:

11	22	33	23,32	31,13	12,21	(тензорные индексы)	(9)
↓	↓	↓	↓	↓	↓
1	2	3	4	5	6	(матричные индексы)

В итоге получим:

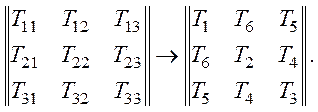
По правилу (9) осуществляется также переход от тензорных к матричным обозначениям и для тензоров более высоких рангов, симметричных по одной или больше пар индексов. Для тензора 3-го ранга, симметричного по последним двум индексам, и, следовательно, имеющего 18 независимых компонент, второй и третий индексы можно по правилу (9) заменить на один, пробегающий значения от 1 до 6.

В развернутом виде тензор представляет собой в матричной записи таблицу из трех строк и шести столбцов (3×6). Примером такого тензора служит тензор пьезоэлектрических модулей.