Если в осях координат X1, X2, X3 вектор 
и вектор 
то
, (1)
т.
е. каждая компонента 
пропорциональна
соответствующей компоненте E.
Если же проводник кристаллический, то отношения между
компонентами и 
не
будут такими простыми, потому что кристаллы по отношению к электропроводности
анизотропны.
Для кристаллов соотношения (1) заменяются следующими:
j1=s11E1+s12E2+s13E3,
j2=s21E1+s22E2+s23E3, (2)
j3=s31E1+s32E2+s33E3,
где s11, s12…s33 − константы.
Каждая компонента 
линейно
зависит от всех трех компонент E, и вектор не совпадает по направлению с .
Каждый из коэффициентов s11, s12…s33 в
уравнениях (2) имеет определенный физический смысл. Например, если поле приложено
вдоль оси x, то 
и уравнения (2)
примут вид j1=s11E1, j2=s21E1, j3=s31E1
Следовательно, теперь компоненты j имеются не только вдоль оси x1 а также и вдоль других осей (x2 и x3 ).
Продольная компонента определяется коэффициентом s21 и s31. Аналогично
коэффициент s23 определяет компоненту ,
параллельную оси x3, когда
поле приложено вдоль оси x3. Итак,
чтобы определить электропроводность кристалла, нужно задать девять
коэффициентов: s11, s12…s33. Для удобства их записывают в виде квадратной
таблицы:
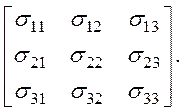
Эта таблица, заключенная в квадратные скобки, обозначает тензор 2-го ранга, а s11, s12…s33. − компоненты тензора. Первый индекс указывает строку, а второй − столбец, в котором стоит компонента. На главной диагонали стоят компоненты s11, s12…s33.
В общем случае, если свойство T
связывает два вектора 
и 
таким
образом, что
p1=T11q1+T12q2+T13q3,
p2=T21q1+T22q2+T23q3,
j3=T31q1+T32q2+T33q3, а
T11, T12… T33 − константы, то они образуют тензор 2-го ранга:
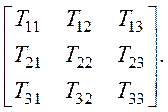
Перейдя к сокращенной записи тензорных соотношений, получим
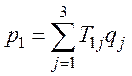
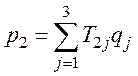или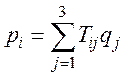 
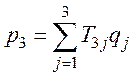i=1, 2, 3.
Опустим знак суммирования:
pi=Tijqj(ij=1, 2, 3). (3)
Если в одном и том же члене уравнения индекс повторяется дважды, то автоматически подразумевается суммирование по этому индексу.
Сравним теперь три типа введенных величин:
1. Тензор нулевого ранга (скаляр) определяется одним числом, не зависящим от выбора осей координат.
2. Тензор 1-го ранга (вектор) определяется тремя числами (компонентами), каждое из которых связано с одной из осей координат.
3. Тензор 2-го ранга определяется девятью числами (компонентами), каждое из которых связано с парой осей координат (взятых в определенном порядке).
Скаляр записывается без индексов (например, плотность ρ).
Компоненты вектора имеют по одному индексу (например, E2), компоненты тензора 2-го ранга − по два индекса (например, s23). Итак, число индексов всегда равно рангу тензора.
Под преобразованием осей координат понимаем переход от
одной системы взаимно ортогональных осей координат к другой с тем же началом.
При этом масштабные коэффициенты вдоль каждой из осей всегда остаются неизменными.
Обозначим первоначальную систему осей координат через
x1, x2, x3 и новую систему через 
.
Углы между новыми и старыми осями определяются направляющими косинусами.
Старые оси
Новые оси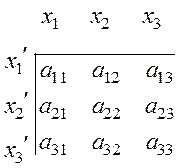 
Например, направляющие косинусы углов между осью 
и осями
x1, x2, x3 равны a21, a22, a23, а направляющие косинусы
углом между осью x3 и осями 
равны a13, a23, a33. Первый индекс при
символе а относится к новым осям, а второй − к старым.
Предположим теперь, что имеем вектор 
с компонентами p1, p2, p3 в системе координат x1, x2, x3. Найдем его компоненты 
в новой системе осей.
Компоненту 
находим,
проектируя на новую ось 
,
т. е.
.
Отсюда
.
Аналогично
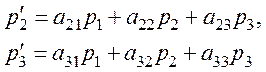
или
.
При обратном преобразовании получим
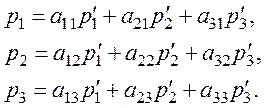
При переходе от старой системы к новой индексы суммирования стоят рядом. При обратном преобразовании индексы суммирования отделены друг от друга. Здесь и далее используется правило суммирования по двум повторяющимся в одном члене одинаковым индексам.
Координаты (x1, x2, x3) точки Pотносительно
системы осей x1, x2, x3 являются одновременно компонентами
вектора 
. На основании этого утверждения
запишем следующее:
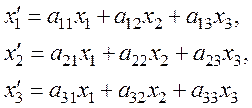
и
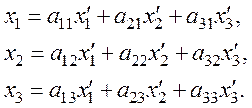
или
В соответствии с (3) имеем pi=Tijqi,
где Tij − тензор 2-го ранга (конкретные значения его компонент Tij зависят от выбранной системы координат (x1, x2, x3).
Векторы и 
в новой системе будут иметь компоненты
и 
.
Найдем соотношения между этими новыми компонентами, используя следующий порядок
уравнений:
Поскольку в качестве индекса суммирования можно взять любую букву, уравнение (1) представим так:
Используя k в качестве свободного индекса, а l в качестве индекса суммирования и заменяя индекс i на l, имеем
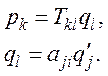
Комбинируя уравнения, получаем
или
Окончательно запишем:
(4)
Уравнение, выражающее старые компоненты тензора через новые, можно получить, используя обратное преобразование с индексами, стоящими в обратном порядке.
В результате
(5)
Аналогично получим выражения для преобразования тензоров более высоких рангов, которые приведены в табл. 3. При преобразовании тензора изменяется не физическая величина, которую описывает тензор (она не зависит от выбора конкретной системы координат), а лишь способ представления этой величины.
Таблица 3
Законы преобразования тензоров
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.