Раздел 7. Проекция Гаусса-Крюгера.
Тема 7.1. элементы геометрии земного эллипсоида.
§1 Радиусы кривизны главных нормальных сечений и параллели, средний радиус кривизны.
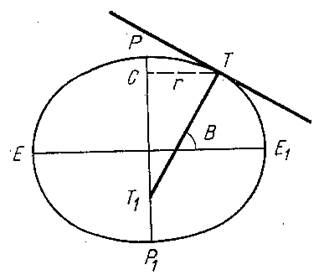
Через нормаль к поверхности эллипсоида можно провести множество плоскостей. Эти плоскости называются нормальными. Кривые, образуемые от пересечения нормальных плоскостей в данной точке, с поверхностью эллипсоида, называются нормальными сечениями. В каждой точке на поверхности эллипсоида есть два взаимно перпендикулярных сечения, кривизна которых имеет максимальное и минимальное значение. Эти нормальные сечения называются главными нормальными сечениями.
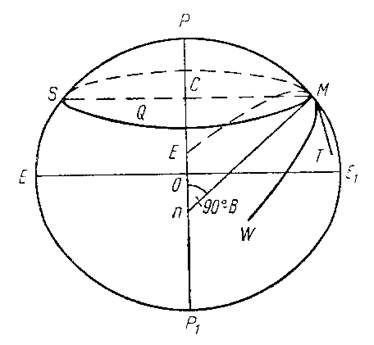 В точке М поверхность эллипсоида
вращения главными нормальными сечениями будут меридианное сечение точки М
и сечение первого вертикала. Эти два сечения представляются эллипсами. Сечение
первого вертикала, проходящее через точку М, будет перпендикулярно
меридианному сечению точки М.
В точке М поверхность эллипсоида
вращения главными нормальными сечениями будут меридианное сечение точки М
и сечение первого вертикала. Эти два сечения представляются эллипсами. Сечение
первого вертикала, проходящее через точку М, будет перпендикулярно
меридианному сечению точки М.
Обозначим через M и N радиусы кривизны меридиана и первого вертикала. Не приводя выводы формул, запишем:
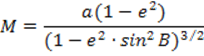
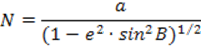
, где: a – большая полуось эллипсоида; e – первый эксцентриситет эллипсоида; B – геодезическая широта точки M.
Из формул видно, что радиусы кривизны возрастают при увеличении широты. Запишем отношение N и M.
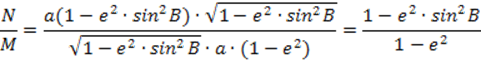
 На полюсе B=90˚,
поэтому на полюсе M и N будут равны. Во всех остальных случаях N больше M.
Если меридиан имеет меньший радиус, то кривизна наибольшая. Радиусом кривизны
первого вертикала является отрезок нормали ТТ1.
На полюсе B=90˚,
поэтому на полюсе M и N будут равны. Во всех остальных случаях N больше M.
Если меридиан имеет меньший радиус, то кривизна наибольшая. Радиусом кривизны
первого вертикала является отрезок нормали ТТ1.
Средним радиусом кривизны в данной точке поверхности называется предел, к которому стремится среднее арифметическое из радиусов кривизны нормальных сечений, когда число их стремится к бесконечности.
Для точек эллипсоида средний радиус кривизны Rравен среднему геометрическому из радиусов кривизны главных нормальных сечений, меридиана и первого вертикала, проведенных для той же точки.
![]()
Радиус кривизны меридиана применяют при вычислении длин дуг меридианов и разности широт.
Разность кривизны первого вертикала применяют при вычислении длин дуг параллелей, разности долгот и азимутов.
Средний радиус кривизны применяют, когда Землю принимают за шар; при вычислении сферических избытков и других случаях.
Если TT1 радиус кривизны первого вертикала, а r – радиус кривизны параллели, проходящей через точку T, то
![]()
§2 Вычисление длин дуг меридианов и параллелей.
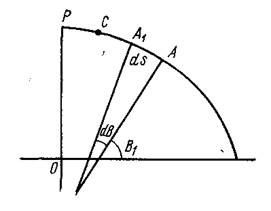
Пусть
требуется определить длину дуги меридиана между точками A и C с широтами
B1
и B2.
Разобьем этот отрезок дуги на бесконечно малые отрезки, тогда дуга малого
отрезка выразится формулой ![]() ,
как малый отрезок дуги окружности радиуса M.
,
как малый отрезок дуги окружности радиуса M.
 Длина всей дуги Ac определится из интегрирования функции
Длина всей дуги Ac определится из интегрирования функции ![]() в
пределах от B1
до B2:
в
пределах от B1
до B2:
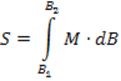
В триангуляции, при длинах дуг свыше 45 км используется формула:
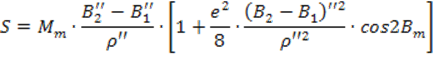
Здесь: Mm – радиус кривизны меридиана для средней широты
![]()
Для длин дуг менее 45 км можно воспользоваться формулой:
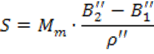
,это означает, что длину дуги можно определить, как дугу центрального угла окружности равном B2-B1.
Длина дуги параллели (окружности) определяется формулой:
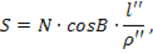
,
где ![]() .
.
§3 Понятие о взаимных нормальных сечениях и геодезической линии.
Возьмем на поверхности эллипсоида две точки A и B, не лежащие на одном меридиане с широтами BA и BС. Широта BС >BA. Проведем нормали в точках A и B. Нормали не пересекаются, так как лежат в разных плоскостях. Широты BA и BСне равны, значит нормали пересекают малую ось эллипсоида в разных местах. Нормаль с более северной широтой пересекает малую ось южнее, чем нормаль с меньшей широтой.
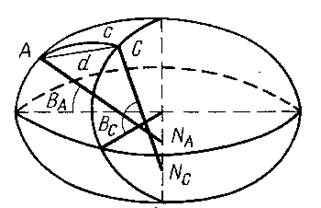 Плоскость, проходящая через нормаль ANA и точку C,
не совпадает с плоскостью, проведенной через нормаль CNC и точку A.
Первая плоскость образует с поверхностью эллипсоида нормальное сечение AAC,
вторая нормальное сечение CCA.
Между двумя точками поверхности эллипсоида проходят два нормальных сечения,
которые называются взаимными нормальными сечениями. Сечение AAC
прямое, а сечение CCA
обратное в точке A.
Плоскость, проходящая через нормаль ANA и точку C,
не совпадает с плоскостью, проведенной через нормаль CNC и точку A.
Первая плоскость образует с поверхностью эллипсоида нормальное сечение AAC,
вторая нормальное сечение CCA.
Между двумя точками поверхности эллипсоида проходят два нормальных сечения,
которые называются взаимными нормальными сечениями. Сечение AAC
прямое, а сечение CCA
обратное в точке A.
Если начальная точка A лежит южнее точки C, то прямое нормальное сечение точки A отклоняется к югу от обратного.
Прямое нормальное сечение можно представить, если в точке A установить теодолит, чтобы его вертикальная ось совпадала с нормалью, то при визировании на вторую точку C, выставленные в створе вешки, обозначат прямое нормальное сечение на поверхности эллипсоида.
При измерении на земной поверхности вертикальная ось теодолита устанавливается по отвесной линии, в то время как прямое нормальное сечение является стороной триангуляции, полигонометрии на поверхности эллипсоида. Значит, при проектировании на поверхность эллипсоида надо вводить поправки за уклонение отвесных линий и за высоту наблюдаемой цели над поверхностью эллипсоида.
В равнинных районах принимают измеренные направления на поверхности Земли такими же и на поверхности эллипсоида. Если по измеренным направлениям составить треугольники, то стороны следует изобразить взаимно обратными нормальными сечениями. Значит, на поверхности эллипсоида не образуется замкнутой фигуры.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.