Проекция Гаусса-Крюгера. Элементы геометрии земного эллипсоида. Радиусы кривизны главных нормальных сечений и параллели, средний радиус кривизны, страница 4

Геодезические координаты, широко применяемые  при изучении фигуры Земли и решении геодезических задач на обширных территориях, оказываются неудобными при выполнении топографических съемок, и решении других инженерно-геодезических задач.

Практическое использование геодезических координат усложняется тем, что их значение вычисляются в градусной мере, а линии на земной поверхности измеряются в линейной мере. Таким образом, возникает необходимость в подборе такой системы координат, которая была бы проста и удобна в применении во всех геодезических работах. Такой системой координат является система плоских прямоугольных координат. В ней решение геодезических задач производится по формулам прямолинейной тригонометрии, но для этого необходимо элементы поверхности эллипсоида перенести на плоскость. Такие проекции должны обеспечивать высокую точность, чтобы возникающие при проектировании искажения нарастали медленно, но можно было учитывать эти искажения по простым формулам.

При выборе плоских прямоугольных координат наиболее выгодной будет равноугольная (конформная) проекция, в которой сохраняются значения углов при переносе с поверхности эллипсоида на плоскость проекции.

Свойство равноугольности обеспечивается тем, что в каждой точке масштаб по всем направлениям будет один и тот же, хотя в разных точках он будет различным. Благодаря этому при проектировании с эллипсоида на плоскость сохраняется подобие бесконечно малых фигур.

§2. Общие сведения о проекции Гаусса-Крюгера.

Теоретическое обоснование конформной проекции дал Гаусс в 1825 году, а в 1912 году Крюгер дал формулы для вычисления в проекции. В СССР система координат была применена впервые Н.Г. Келль при обработке триангуляции Кузбасса и начиная с 1928 года эта проекция принята в качестве общесоюзной системы координат при топографо-геодезических работах. Поперечно-цилиндрическую проекцию Гаусса можно представить как эллипсоид, вписанный в цилиндр, чтобы один из меридианов касался стенок цилиндра. Этот меридиан назовем осевым. Образующие цилиндра будут 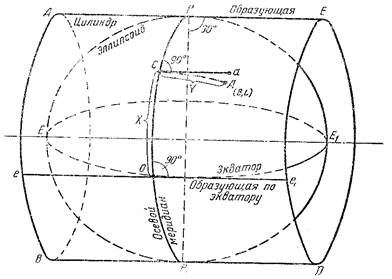перпендикулярны к осевому меридиану, ось цилиндра проходит через центр эллипсоида. Спроектируем из центра эллипсоида точки земной поверхности на стенки цилиндра, а затем развернем его  в плоскость. Получим плоское изображение земной поверхности, которое будет конформной поперечно-цилиндрической проекцией Гаусса. Осевой меридиан и экватор, как взаимно перпендикулярные нормальные сечения изобразятся взаимно перпендикулярными прямыми примем их за оси координат. Точка их пересечения  является началом системы координат.

Положение точки  на плоскости соответствует точка  на эллипсоиде. Координаты точки  будут , которые называются плоскими прямоугольными координатами Гаусса.

По мере удаления от осевого меридиана цилиндр все больше отступает от поверхности эллипсоида, что влечет увеличение искажений.

Чтобы избежать недопустимых искажений, поверхность эллипсоида делят меридианами на 6˚ зоны. Зоны представляют собой двуугольники, вершины располагаются в полюсах. Каждая из этих зон проектируется на цилиндр отдельно, чтобы осевой меридиан соприкасался со стенками цилиндра. Осевой меридиан и экватор являются осями координат.

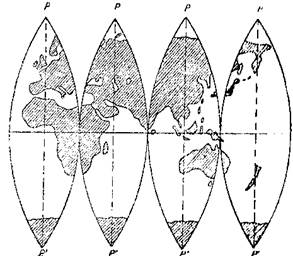В нашей стране за основную систему зон принята 6˚ градусная зона. В каждой зоне свои координаты, связь между ними осуществляется через геодезические координаты. Счет зон начинается от Гринвичского меридиана на восток. Зоны совпадают с колоннами листов международной карты М 1:1000000. Долгота осевого меридиана L₀ вычисляется по формуле:

, где n– номер зоны.

При создании крупномасштабных карт используют трехградусные зоны. Осевыми меридианами таких зон являются осевые и крайние меридианы шестиградусных зон.

Координаты X отсчитываются от экватора, а Y – от осевого меридиана зоны. К востоку от осевого меридиана они положительные, к западу – отрицательные. Чтобы не иметь дело  с отрицательными координатами, к координатам Yприписывают 500 км и дописывают впереди номер зоны. Это будут преобразованные координаты, например: