Проекция Гаусса-Крюгера. Элементы геометрии земного эллипсоида. Радиусы кривизны главных нормальных сечений и параллели, средний радиус кривизны, страница 8

Практический пример.

Дано:

Вычислить прямоугольные координаты в зоне с осевым меридианом  .  В последней задаче мы по координатам   и  вычислим геодезические координаты, возьмем их в качестве исходных, а долготу осевого меридиана возьмем 27˚

Номер действия	Формулы	Результаты
1	L1	24˚02ˊ13.1360ˊˊ
2	L0	27˚
3	B0ˊ	51˚38ˊ43.9023ˊˊ
4	B1ˊˊ	185923.9023ˊˊ
5	B1ˊˊ/ρˊˊ	0.901384542
6	sin B1	0.7841868
7	cos B1	0.6205248
8	cos2 B1	0.3850510
9	l˚=L1-L0	-2˚57ˊ46.864ˊˊ
10	lˊˊ	-10666.864ˊˊ
11	l, рад	-0.051714418
12	N	6391412.451
13	a0	32088.400
14	a4	0.05497637
15	a6	-0.00773241
16	a3	-0.03814988
17	a5	-0.02648123
18	sin B1 cos B1	0.4866073
19	l2	0.002674381
20	N l2	17093.071944
21	6367558.4969 Bˊˊ/ρˊˊ	5739618.8000
22	xII	5728164.378 м.
23	1+( a3+ a5l2) l2	0.99989778
24	[23]lcosB1	-0.03208680
25	yII	-205079.963 м.
		294920.037 м.

§8. Сущность и последовательность  переноса геодезической сети с эллипсоида на плоскость в проекции Гаусса – Крюгера.

При переносе сторон треугольников с поверхности эллипсоида на плоскость в проекции Гаусса изображается кривыми, вогнутостью направленными в сторону оси абсцисс. Углы между этими кривыми, по условию равноугольности проекции равны измеренным  на местности.

Чтобы иметь возможность решать треугольники по правилам прямолинейной тригонометрии, в направления вводят поправки за кривизну геодезических линий.

Исходными данными для переноса сети триангуляции служат широты и долготы пунктов, длины базисных сторон  и азимуты этих сторон, а также измеренные на местности углы. Последовательность переноса сетей:

1.  По известным геодезическим координатам вычисляют прямоугольные координаты и Гауссово сближение меридиана.

2.  Вычисляем приближенный дирекционный угол базисной стороны

3.  Вычисляем поправку за проектирование базисной стороны на поверхность эллипсоида, а затем вычисляют и  длину стороны

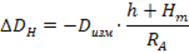
, где

 - превышение квазигеоида над эллипсоидом;

 -средняя высота линии над уровнем Балтийского моря.

 - радиус кривизны земного эллипсоида, выбирается из таблиц по широте  и азимуту  линии

4.  Вычисляем координаты конечной точки базисной стороны

5.  Имея координаты обоих концов базисной стороны, вычислим окончательный дирекционный угол

6.  Длину базисной стороны редуцируем на плоскость

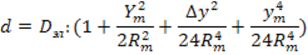
7.  Вычисляем приближенные координаты всей сети и поправки за кривизну геодезических линий по формуле

Получаем редуцированные на плоскость направления.

Раздел 9. Уравнивание геодезических сетей.

Тема 9.1 Основы метода наименьших квадратов.

§1. Сущность задачи уравнивания геодезических сетей и ее решение по методу наименьших квадратов.