Проекция Гаусса-Крюгера. Элементы геометрии земного эллипсоида. Радиусы кривизны главных нормальных сечений и параллели, средний радиус кривизны, страница 15

2.  Вычисление приближенных дирекционных углов и коэффициентов  и  для нетвердых направлений.

Приближенные дирекционные углы получают из решения обратной геодезической задачи по формуле:

, используя шестизначные таблицы натуральных значений тригонометрических функций. Для контроля вычисляют дирекционный угол (45˚+α) по формуле

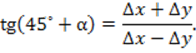
Коэффициенты a и b вычисляем по формуле:

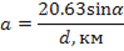
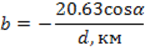
Таблица №4

Элементы  Название  1 формул       пунктов   2	D A	D B	D C
X2 X1 ΔX= X2- X1 Y2 Y1 ΔY= Y2- Y1 tgα= ΔY/ ΔX α ΔX+ ΔY ΔX- ΔY tg(45˚+α) 45˚+α cos α sin α d= ΔX/ cos α= ΔY/ sin α a b	6114256.42 6117470.71 -3214.29 7282749.44 7286341.84 -3592.40 1.117634 228˚10ˊ46.3ˊˊ -6806.69 +378.11 -18.001877 273˚10ˊ46.2ˊˊ -0.66680 -0.74524 4820 м -3.19 +2.85	6124055.26 6117470.71 +6584.55 7287996.75 7286341.84 +1654.91 0.251332 14˚06ˊ29.0ˊˊ +8239.46 +4929.64 +1.671412 59˚06ˊ29.0ˊˊ +0.96984 +0.24375 6789 м +0.74 -2.95	6114518.77 6117470.71 -2951.94 7289756.85 7286341.84 +3415.01 -1.156870 130˚50ˊ24.8ˊˊ +463.07 -6366.95 -0.072730 175˚50ˊ24.7ˊˊ -0.645395 +0.75654 4514 м +3.46 +2.99

3.  Вычисление свободных членов уравнений поправок.

Имея дирекционные углы всех направлений и измеренные углы, вычисляют свободные члены уравнений поправок по формуле:

l = (α₂ˊ- α₁ˊ) - Mˊ, где

α₁ˊ и α₂ˊ - приближенные дирекционные углы, Mˊ - измеренный угол.

Пример вычислений дан в таблице №5.

Контроль вычислений свободных членов: сумма свободных членов управлений поправок по треугольникам должна равняться невязке треугольника с обратным знаком:

l₁+ l₂+ l₃ = -W

Например, из таблицы №5 выбираем l для первого треугольника: -3.0ˊˊ+1.9ˊˊ- 0.9ˊˊ= -2.0ˊˊ, из таблиц №2: W₂ = +2.0ˊˊ

Таблица №5

Назван. пункт.	Назв. напр.	Дирекц. углы αˊ	№№ углов	Вычисл. углы Mαˊ= α2ˊ- α1ˊ	Измер. углы Mˊ	Своб. чл. l
D A B	A B C B D C D A D B	228˚10ˊ46.3ˊˊ 14˚06ˊ29.0ˊˊ 130˚50ˊ24.8ˊˊ 28˚10ˊ09.1ˊˊ 48˚10ˊ46.3ˊˊ 169˚32ˊ34.4ˊˊ 194˚06ˊ29.0ˊˊ 208˚10ˊ09.1ˊˊ 310˚50ˊ24.8ˊˊ 349˚32ˊ34.4ˊˊ	2 6 1 4 3 5	145˚55ˊ42.7ˊˊ 116˚43ˊ55.8ˊˊ 20˚00ˊ37.2ˊˊ 24˚33ˊ54.6ˊˊ 14˚03ˊ40.1ˊˊ 38˚42ˊ09.6ˊˊ	145˚55ˊ40.8ˊˊ 116˚43ˊ58.1ˊˊ 20˚00ˊ40.2ˊˊ 24˚33ˊ53.9ˊˊ 14˚03ˊ41.0ˊˊ 38˚42ˊ05.2ˊˊ	+1.9 -2.3 -3.0 +0.7 -0.9 +4.4

4.  Составление уравнений поправок.

Число уравнений поправок будет равно числу непосредственно измеренных углов. В нашем примере их будет 6. В общем виде уравнение поправки в измеренный угол  записывается так:

, где

 - поправка в измеренный угол ;

; ;   - поправки в абсциссы пунктов  A, B, Dвыраженных в дециметрах.

; ;  – поправки в ординаты пунктов A, B, D.

 - свободный член уравнения.

Для угла  в окончательном варианте уравнение поправок будет:

Остальные члены уравнения  будут равны нулю, т.к. пункты  - твердые.

5.   Составление нормальных уравнений.

Для вычисления коэффициентов нормальных уравнений заполняют таблицу коэффициентов уравнений поправок (таблица №6), в которой впоследствии вычисляются поправки υ.