Проекция Гаусса-Крюгера. Элементы геометрии земного эллипсоида. Радиусы кривизны главных нормальных сечений и параллели, средний радиус кривизны, страница 14

§3. Уравнивание сети триангуляции параметрическим способом.

В параметрическом способе уравнивания на основании функциональных зависимостей между определенными неизвестными и измеренными величинами составляют уравнения поправок.

Сущность способа уравнивания заключается в следующем: сначала вычисляем приближенные значения координат определяемых пунктов, а затем составляют уравнения поправок для всех измеренных углов и линий.

Поправки в измеренные углы получаем через поправки координат.

Последовательность уравнивания параметрическим способом:

1.  Определяем число избыточных измерений.

2.  Выбираем параметры, чтобы они не имели математических связей между собой. Параметрами могут являться непосредственно измеренные углы треугольника и стороны, а также координаты пунктов. Число таких параметров должно равняться числу необходимых измерений. Важно, чтобы параметрические уравнения поправок, составленные с помощью этих параметров, были простые.

3.   Все измеренные величины выражают в виде функций выбранных параметров

, где 

4.  Находим приближенные значения параметров  .

5.  Приводим функции к линейному виду, а для этого, вычисляем коэффициенты и свободные члены параметрических уравнений поправок.

6.  Составляем и решаем систему нормальных уравнений, в результате чего получаем поправки  .

7.  Вычисляем значение поправок   в результаты измерений.

8.  Находим  уравненные значения измеренных величин и параметров

9.  Осуществляем контроль выполненного уравнивания.

А теперь рассмотрим уравнивание на конкретном примере:

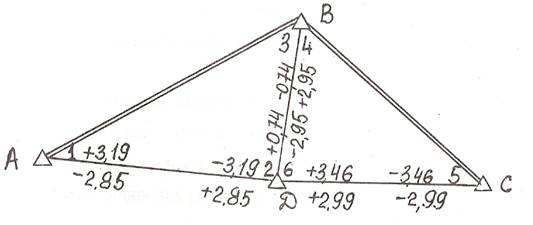
Примечание: по каждому нетвердому направлению выписаны коэффициенты a и b направлений (см. таблицу №4)

Исходные данные.

Таблица №1

Измеренные и окончательно уравненные углы

Таблица №2

Примечание: поправки υ и уравненные углы Mˊ+ υ записывают в таблицу №2 после решения нормальных уравнений (таблица №8) и вычисления поправок (таблица №6).

1.  Вычисление приближенных координат определяемых пунктов.

Координаты вычисляют по формуле Юнга, используя углы треугольников, исправленные поправки за счет распределения невязок треугольников поровну на каждый угол треугольника.

Вычисление приближенных координат пункта  по формулам Юнга.

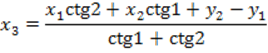
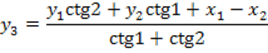
Таблица №3

Назван. пунктов	Предв. урав. углы	x	ctg 2 ctg 1	y
B A D C B D	14˚03ˊ40.3ˊˊ 20˚00ˊ39.6ˊˊ 38˚42ˊ06.2ˊˊ 24˚33ˊ54.8ˊˊ Среднее xDˊ	6124055.26 6114256.42 6117470.61 6114518.77 6124055.26 6117470.81 = 6117470.71	+2.745830 +3.992610 +6.738440 +2.187690 +1.248128 +3.435818 yDˊ	7287996.75 7282749.44 7286341.83 7289756.85 7287996.75 7286341.84 = 7286341.84