Проекция Гаусса-Крюгера. Элементы геометрии земного эллипсоида. Радиусы кривизны главных нормальных сечений и параллели, средний радиус кривизны, страница 7

§4.  Перенос линий с поверхности эллипсоида на плоскость.

Геодезическая линия (нормальное сечение) длиной   на плоскости в проекции Гаусса изображается кривой  .

Обозначим бесконечно малые отрезки этих линий через  и . Из определения масштаба можно написать:

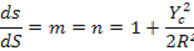
Заменим сферическую ординату  ординатой Гаусса, тогда получим:

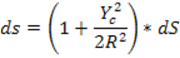
Небольшие по длине линии 10-15 км можно практически считать бесконечно малыми в сравнении с размерами Земли.

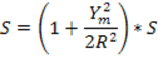
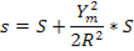
Радиус   можно брать для средней широты.

Величина:

всегда положительная, поэтому линия на плоскости всегда больше  линии на эллипсоиде.

Углы  и  слишком малые, практически можно принять длину хорды равной длине кривой.

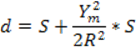
Этой формулой можно пользоваться в 3 и 4 кл. В триангуляции 1 кл надо применять более точную формулу:

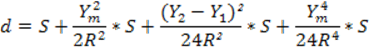
§5.  Перенос направлений с поверхности эллипсоида на плоскость.

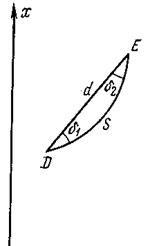
Стороны треугольников при переносе с поверхности эллипсоида на плоскость изображаются дугами вогнутостью направленными в сторону оси абсцисс.

Углы между этими кривыми (касательными к кривым в вершине угла) по условию равноугольности равны измеренным на местности.

Чтобы иметь возможность решать треугольники по правилам прямоугольной тригонометрии, от криволинейных сторон переходим к прямолинейным, заменяя кривые хордами.

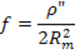
Координаты берем в км, до сотых долей, от координаты  отбрасываем зону и вычитаем 500 км.

Поправку δ нужно всегда прибавлять к измеренным направлениям.

Обозначим измеренные направления через , редуцированные направления через . Тогда в треугольнике редуцированные углы будут:

Складываем, левые и правые части равенств, получим:

Или

Вычислив поправки в направления за кривизну геодезических линий, можно вычислить дирекционный угол.

На чертеже:

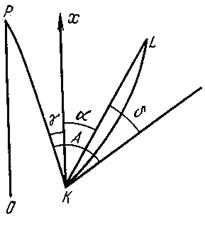А - геодезический азимут;

γ - сближение меридианов;

α - дирекционный угол геодезической линии;

δ - редукция направления

Сумма поправок в углы треугольника должна равняться сферическому избытку с обратным знаком.

§6. Гауссово сближение меридианов.

На рисунке - осевой меридиан зоны;

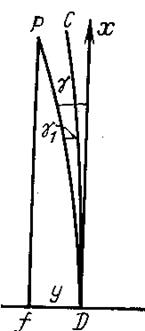
- меридиан точки ;

- линия, параллельная осевому меридиану на поверхности эллипсоида;

-ордината точки ;

- сближение меридиана на эллипсоиде;

- сближение меридиана на плоскости. Это угол между изображением меридиана и направлением, параллельным оси   в данной точке.

Приближенная формула для вычисления γ будет:

,где

Погрешность вычисления по этой формуле, на краю шестиградусной зоны не превышает 4", на краю трехградусной зоны не более . Максимальное значение γ в шестиградусной зоне не превышает 3˚

Точная формула:

Сближение меридианов выполняют обычно при вычислении плоских координат. Знак сближения меридиана совпадает со знаком .

Вторая формула:

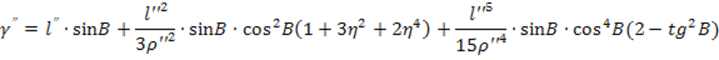
где:

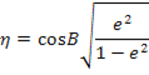
§7. Преобразование прямоугольных координат Гаусса – Крюгера из одной 6˚ зоны в другую 6˚ зону.

Необходимость решения данной задачи возникает, когда геодезические работы выполняются на стыке двух смежных зон, т.е. координаты начального и конечного пунктов даны в разных зонах.

Самый простой способ – это по координатам  и  вычисляем геодезические координаты   и , затем по геодезическим координатам и осевому меридиану соседней зоны вычисляем  и . Эти вычисления требуют значительного времени и применяют его, когда нужно преобразовать небольшое количество пунктов.

Второй способ заключается в следующем. От редуцированных направлений и сторон на плоскости в первой зоне перейдем к направлениям и сторонам на сфере, а от них – к редуцированным направлениям и сторонам в системе второй зоны и вычислению искомых координат пунктов в этой( второй) зоне по обычным формулам.

Чтобы избежать многократных одних и тех же вычислений в 30 зоне, к востоку и западу от граничных меридианов, в каталогах помещают координаты в двух зонах.

Для упрощения вычислений применяются специальные таблицы, например:

1. С.П.Герасименко и А.В. Бутковича

2. Е.Е.Бирюкова

3. Вировца А.М. и Б.Н. Рабиновича, и другие