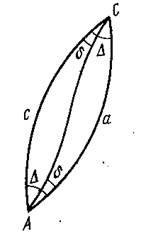
 Величина угла Δ между взаимными
нормальными сечениями небольшая и зависит от длины линии S,
ее азимута A и широты B.
Так при B=60˚,
A=50˚
при:
Величина угла Δ между взаимными
нормальными сечениями небольшая и зависит от длины линии S,
ее азимута A и широты B.
Так при B=60˚,
A=50˚
при:
· S=30 км Δ=0,004"
· S=100 км Δ=0,032"
При положении пунктов на одном меридиане или на одной параллели взаимные нормальные сечения сливаются в одну линию.
В триангуляции 2,3,4 класса двойственностью нормальных сечений пренебрегают.
В триангуляции 1 класса двойственность нормальных сечений устраняют тем, что пункты соединяют геодезическими линиями. Геодезическая линия – это кривая, являющаяся кратчайшим расстоянием между двумя точками на поверхности эллипсоида.
Геодезическая линия в точках A и C располагается к прямым нормальным сечениям и составляет с ним угол δ равный 1/3 Δ.
§4 Сферический избыток треугольника.
Стороны триангуляции по сравнению с размерами эллипсоида весьма малы, поэтому при обработке триангуляции сфероидические треугольники можно без ощутимых погрешностей в углах и длин сторон принять за сферические. Как известно радиус сферы в этом случае принимают равным.
![]()
Стороны сферических треугольников - это дуги больших кругов сферы. Такие треугольники решают по формулам сферической тригонометрии.
Однако
малые сферические треугольники, какими являются треугольники триангуляции,
удобнее решать не как сферические, а как плоские, по теореме Лежандра.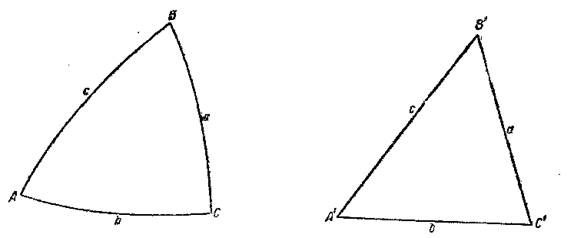
Пусть
дан сферический треугольник ![]() со
сторонами
со
сторонами ![]() Построим
плоский треугольник
Построим
плоский треугольник ![]() ,
чтобы его стороны были равны сторонам сферического треугольника. Используем
формулы Лежандра без доказательства для малых треугольников
,
чтобы его стороны были равны сторонам сферического треугольника. Используем
формулы Лежандра без доказательства для малых треугольников
![]()
![]()
![]()
Сложим эти выражения:
![]()
В плоском треугольнике:
![]()
Поэтому
![]()
Здесь:
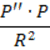
– Называется
сферическим избытком, ![]()
Чтобы получить плоский угол надо:
![]()
![]()
![]()
Углы
![]() -
плоские приведенные. По теореме синусов вычислим стороны плоского треугольника
-
плоские приведенные. По теореме синусов вычислим стороны плоского треугольника
![]()
Пусть
сторона ![]() известна
известна
![]()
![]()
Площадь плоского треугольника
![]()
По малости сферических избытков сферические углы заменены на плоские. Таким образом, сферический избыток равен:
![]()
Обозначим:
![]()
, тогда
![]()
Сферический
избыток при сторонах меньше 30 км не превышает ![]() .
При вычислении стороны выражаем в километрах, до сотых долей.
.
При вычислении стороны выражаем в километрах, до сотых долей.
Величина f является функцией широты B
На широте B=35˚ f= 0.00254
B=55˚ f= 0.00253
B=75˚ f= 0.00252
Пример:
Дано: A = 50˚20ˊ19.41ˊˊ b = 44797.282 м
B = 62˚12ˊ44.54ˊˊ Bm = 48˚12ˊ
C= 67˚26ˊ58.43ˊˊ
1.
![]()
2. Вычисление сферического избытка
![]()
![]()
![]()
Обозначим выражение
![]()
, тогда
![]()
f = 0.00253
![]() 1426.95
1426.95
b2 = 2007.04 sin B =0.884681
sin A =0.760831 D1= 1612.95
sin C = 0.923542 ![]() 4.086ˊˊ
4.086ˊˊ
![]() 4.09
4.09
![]() 0.710971
0.710971
3. Пусть
![]()
![]()
![]()
![]()
b = 44797.282 м
![]()
![]()
![]()
4. Решение треугольника
|
Вершина |
измеренные углы сферического треугольника |
Поправка
на |
Уравненные углы сферического треугольника |
|
Углы плоского треугольника |
sin углов плоского треугольника |
|
B A C |
62˚12ˊ44.54ˊˊ 50˚20ˊ19.41ˊˊ 67˚26ˊ58.43ˊˊ |
0.57 0.57 0.57 |
62˚12ˊ45.11ˊˊ 50˚20ˊ19.98ˊˊ 67˚26ˊ59.00ˊˊ |
-1.36 -1.36 -1.37 |
62˚12ˊ43.75ˊˊ 50˚20ˊ18.62ˊˊ 67˚26ˊ57.63ˊˊ |
0.88467988 0.76982866 0.92354082 |
|
∑ Ε ω |
180˚00ˊ02.28ˊˊ 04.09 -1.71 |
180˚00ˊ04.09ˊˊ |
180˚00ˊ00.00ˊˊ |
Тема 7.2. Общие сведения о картографических проекциях.
§1 Основы классификации проекций.
Поверхность эллипсоида не может быть развернута в плоскости без разрывов и складок, поэтому она отображается с какими-то искажениями.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.