Проекция Гаусса-Крюгера. Элементы геометрии земного эллипсоида. Радиусы кривизны главных нормальных сечений и параллели, средний радиус кривизны, страница 9

Конечной целью обработки триангуляции является вычисление координат пунктов и расстояние между ними. В геодезической практике все измерения выполняются с контролем. Например, для решения треугольников надо бы измерять только два угла в треугольнике, мы же измеряем все три угла, то же происходит с исходными данными, обычно их больше, чем необходимо. Результаты измерений содержат всегда какие-то погрешности. Поэтому всегда возникает неопределенность, т.е. много вариантов решения задачи. Значит после предварительной обработки результаты угловых измерений должны подвергнуться уравнительным вычислениям, которые заключаются в определении вероятнейших значений.

Чтобы вычислить координаты пунктов сети необходимо иметь:

- координаты двух пунктов и по два измеренных угла в каждом треугольнике. Если в сети имеется   пунктов, из которых два исходные, а    пункта надо определить, то для их определения потребуется измерить , если измеренных углов будет , то число   будет избыточно измеренные углы. Но имея избыточные углы,  они не будут лишними. Избыточные измерение используем для проверки качества полевых работ, например, сумма углов в треугольнике должна быть 180˚, если невязка недопустимая, значит надо перенаблюдать. Избыточные измерения нужны для оценки качества измерений. Как распределить поправки в углы треугольника, если произвольно, то может оказаться, что они будут далеки от истинных. Поэтому при обработке триангуляции вводят дополнительные требования, чтобы сумма квадратов поправок к непосредственно измеренным величинам была минимальной.

Этот метод называется «способом наименьших квадратов»

При неравноточных измерениях это уравнение имеет вид:

В теории математической обработки геодезических измерений применяются два основных способа:

- коррелатный (способ условий или условных измерений);

- параметрический (способ посредственных измерений).

§2  Коррелатный способ уравнивания.

Коррелатный способ уравнивания предусматривает следующую последовательность решения задачи:

1.  Определяем число необходимых и избыточных измерений.

2.  Составляют независимые условные уравнения.

Несоблюдение этого требования обуславливает неопределенность решения задачи уравнивания.

3.  Вычисляют коэффициенты и свободные члены условных уравнений поправок.

4.  Находим коэффициенты нормальных уравнений коррелат.

5.  Решают нормальные уравнения, и получаем коррелаты  .

6.  Определяем поправки   в измеренные величины.

7.  Вычисляют уравненные значения измеренных величин.

8.  Контроль выполненного уравнивания

Пример уравнивания сети триангуляции коррелатным способом.

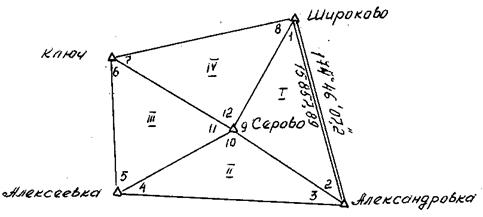
Исходные данные:

Широково:        X=6120691.68 м

Y=7548684.93 м

Александровка: X =6104899.84 м

Y =7550130.81 м

Углы на плоскости помещены в таблице вычисления невязок треугольников. Данная сеть свободная, число условных уравнений подсчитаем по формуле:

, где -число измеренных углов;

- число определяемых пунктов.

=12-10+4=6

Виды условных уравнений:

1.  Условных уравнений фигур – 4

2.  Условных уравнений полюса – 1

3.  Условных уравнений горизонта – 1

Вычисление невязок треугольников.

Таблица №1