Проекция Гаусса-Крюгера. Элементы геометрии земного эллипсоида. Радиусы кривизны главных нормальных сечений и параллели, средний радиус кривизны, страница 16

В таблице №6 на каждой строчке выписывают значение коэффициентов уравнений поправок a и b, и свободные члены l, и подсчитывают сумму S, которая будет использоваться для контроля правильности вычисления коэффициентов нормальных уравнений.

Число нормальных уравнений равно числу поправок в координаты определенных пунктов. В приведенном примере один определяемый пункт D и поэтому число уравнений будет 2 (неизвестные поправки – в абсциссу δ_D и ординату Δ_D).

Таблица №6

№ попр.	a	b	l	S	υˊˊ
1 2 3 4 5 6	δD = +0.179 -3.19 +3.93 -0.74 +0.74 -3.46 2.72	ΔD = +0.511 +2.85 -5.80 +2.95 -2.95 -2.99 +5.94	-3.00 +1.90 -0.90 +0.70 +4.40 -2.30	-3.34 +0.03 +1.31 -1.51 -2.05 +6.36	-2.11 -0.36 +0.48 -0.68 +2.25 +1.23

[υυ] = 11.84

[ll2] = 11.86

[al] δ_D + [bl] Δ_D + [ll] = 11.86

Таблица №7

6.  Решение нормальных уравнений поправок по схеме Гаусса.

Таблица №8

	δx	ΔD	l	S	Контр.
N1 Ԑ1 N2 Ԑ12N1 N2ˊ Ԑ2 N3 Ԑ13N1 Ԑ23N2ˊ N3ˊ δD=	+46.09 -1 ΔD = +0.179	-9.75 +0.212 +103.39 -2.07 +101.32 -1 [ll2]= +0.511 +0.108	-3.26 +0.071 -51.11 -0.69 -51.80 +0.511 +38.56 -0.23 -26.47 +11.86 +0.511 +0.071	+33.08 -0.718 +42.53 +7.01 +49.54 -0.489 -15.81 +2.35 +25.31 +11.85	-0.717 +49.52 -0.489 +11.86

7.  Вычисление уравненных координат пункта .

X_Dˊ = 6117470.71         Y_Dˊ =7286341.84

0.1δ_D = +0.02               0.1 Δ_D = +0.05

X_D = 6117470.73         Y_Dˊ = 7286341.89

8.  Вычисление поправок в измеренные углы и вычисление уравненных углов.

Поправки в измеренные углы вычисляем по уравнениям поправок, которые в общем виде будут:

9.  Оценка точности.

а) средняя квадратическая погрешность измерения угла (ошибка единицы веса) вычисляется по формуле:

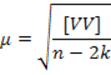
, где n – число всех измеренных углов; k – число определяемых пунктов.

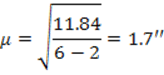
б) средняя квадратическая погрешность определения координат пункта D равна:

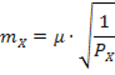
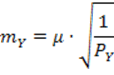
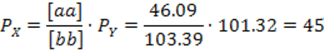
§3 Параметрический способ уравнивания.

Рассмотрим этот способ уравнивания на примере уравнивания нивелирной сети.

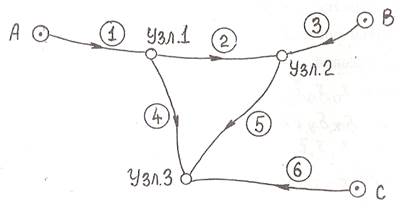
Эта сеть несвободна.

Исходные данные.

                                                                                                    Таблица №1

В параметрическом способе сначала вычисляем приближенные значения отметок трех узловых точек, а для этого обозначим отметки узловых точек через  

Искомые поправки к ним: 

Тогда уравненные отметки:

=247.069+2.128=249.197 м

=248.613+0.563=249.176 м

=250.970-3.013=247.957 м

Составим уравнение поправок.