Проекция Гаусса-Крюгера. Элементы геометрии земного эллипсоида. Радиусы кривизны главных нормальных сечений и параллели, средний радиус кривизны, страница 5

X = 6324547 м.

Y = 3613847 м.

Здесь «3» - номер зоны и точка располагается, к востоку от осевого меридиана на удалении 113847 м от него.

На экваторе значение ординаты в пределах зоны будет:

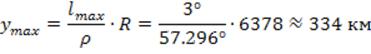
Для территории нашей страны y не превышает  270 км. Основные характеристики и достоинства проекции Гаусса:

1.  Благодаря введению зон, искажения в проекции Гаусса на краю зон сравнительно небольшие и они просто и точно определяются и учитываются.

2.  Проекция Гаусса равноугольная m= n.

3.  Осевой меридиан и экватор изображаются прямыми линиями.

4.  Масштаб вдоль осевого меридиана равен единице.

5.  Меридианы и параллели изображаются дугами.

6.  Главные направления совпадают с направлениями, параллельными осям координат. 

§3. Прямоугольные сферические координаты.

В системе прямоугольных сфероидических координат на поверхности эллипсоида за ось X принимаем  меридиан, проходящий через какую-то точку, выбранную за начало координат. Это может быть любая точка, имеющая геодезические координаты В и L. За ось X принимается осевой меридиан зоны.

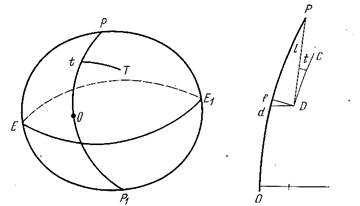Положение точки Т  определится ординатой Tt  и абсциссой Ot. Ордината – дуга Tt первого вертикала в точке t, т.е. геодезическая линия, проходящая от точки T до меридиана, принятого за ось X под прямым углом к нему.

Абсцисса – дуга Ot меридиана от принятого начала координат до основания ординаты. Абсциссы положительны к северу от начала координат и отрицательно к югу от него. Ординаты положительны к востоку от оси X и отрицательны к западу от нее.

На правом чертеже PO – осевой меридиан зоны с долготой L₀. Точка Dна поверхности эллипсоида с широтой B и долготой L.  Точка O – пересечение осевого меридиана с экватором.

Df– дуга первого вертикала в точке fи является сферической ординатой точки D:

Df = y_c

Dd – параллель точки D

DC– линия, параллельная осевому меридиану PO, т.е. дуга сечения сфероида плоскостью параллельной плоскости осевого меридиана.

Of – сферическая абсцисса точки D, обозначим ее через X_c.

T– Геодезическое сближение меридианов.

Тема 7.4. Перенос геодезических сетей с эллипсоида на плоскость и преобразование прямоугольных координат.

§1. Масштаб и условие равноугольности в проекции Гаусса-Крюгера.

Для полосы шириной около 200 км между двумя параллелями поверхность эллипсоида можно принять за поверхность шара с радиусом    

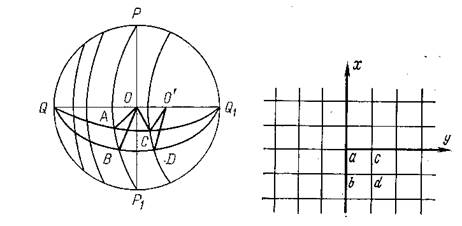На рисунке  - осевой меридиан; – большой круг, полученный от сечения сферы плоскостью перпендикулярной осевому меридиану.  - экватор. Проведем большой круг  , который перпендикулярен осевому меридиану и через равные интервалы малые круги параллельно осевому меридиану.

В соответствии с условием проекции,  проекции равно  сферы. Малые круги изобразятся кривыми, кривизной  их можно пренебречь, их можно принять доля простоты вывода параллельными оси , расстояние между ними равны по построению и равны  соответствующим дугам шара (сферические ординаты равны ординатам на плоскости)

На чертеже видно, что расстояние между экватором и большим кругом при удалении от осевого меридиана уменьшаются. В то же время на проекции они равны. Определим масштаб по оси .

r- Радиус малого круга

( Дуги на сфере, стягиваемы одним двухгранным углом, пропорциональны своим радиусам)

Угол  – центральный, определяется отношением:

или

 =    как накрест лежащие при параллельных прямых.

Из прямоугольного треугольника  , - гипотенуза, равная  . Определим r

, тогда

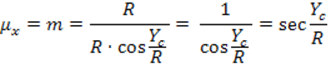
Разложим

в ряд, имеющий вид:

Ограничимся двумя членами разложения, получим:

Под этим условием вычисляются ординаты точек по их прямоугольным сфероидическим величинам.

В каждой точке проекции бесконечно малый элемент ординаты надо увеличивать во столько же, во сколько проектированием увеличивается малый элемент абсциссы.

Вывод:  в проекции Гаусса масштаб  в каждой точке зависит от ординаты точки и искажения возрастают по мере удаления от осевого меридиана зоны.