Численные методы, теория функций комплексного переменного, дискретная математика. Интерполяция и численное дифференцирование

Тогда все слагаемые, кроме одного, не содержащего разности u − v v( = 0,1,...,k k, ≠ 0) будут равны нулю. И

                                                                                ⎧           k          1

⎪ω_k ( )u ^∑s=0 u − s, åñëè u ≠ v,

⎪

                                        ω′( )u = ⎨ k                                                                                        (1.20)

                                                                                ⎪∏(u − s),    åñëè   u = v,

⎪ s=0 ⎩ s v≠

v = 0,1,...,k k; ≠ 0.

          Полученные формулы позволяют вычислить приближённые значения производной при любом количестве узлов. В частности, при двух узлах интерполирования (линейная интерполяция)

1

                                                         f ′( )x = ∆y₀ .                             (1.21)

h

           При трёх узлах интерполирования (квадратичная интерполяция)

                                                               1 ⎡          2u −1   ^{2        ⎤                   1    2}

f ′( )x = _⎢∆y₀ + ₂ ∆ y_0⎦⎥, f ′′( )x = _h2 ∆ y₀ . (1.22) _{h ⎣}

При наличии четырёх узлов интерполирования формулы для производных примут вид:

                                                              1 ⎡          2u −1   ₂              3u² − 6u + 2   ₃        ⎤

f ′( )x =        ⎢∆y₀ +       ∆ y₀ +         ∆ y₀⎥, h ⎣         2        6        ⎦

1      ^{2                  3}         f ′′( )x =       2 ⎡_⎣∆ y₀ + (u −1)∆ y₀⎤_⎦,             (1.23)

_h

                                                                 1    ³

                                           f ′′′( )x = ₃ ∆ y₀.

h

Если производная вычисляется в нулевом узле, то u = 0 и формулы (1.23) приобретают вид:

                                                                                 1⎛          1   2               1   3        ⎞

f ′( )x =       ⎜∆y0 −       ∆ y0 +       ∆ y0 ⎟, h⎝       2        3       ⎠

1    ^{2                  3}         f ′′( )x =       ₂ (∆ y₀ − ∆ y₀ ),               (1.24)

h

                                                                                  1    ³

                                                             f ′′′( )x = ₃ ∆ y₀.

h

Ошибка при вычислении производных существенно увеличивается при увеличении порядка производной, поэтому обычно для вычисления производных порядка выше третьего этот метод не используется.

 Пример 1.2. Функция задана табл. 1.5.                                      Таблица 1.5.

x	0	0,1	0,2	0,3
y	1	1,221	1,491	1,822

Вычислить производные y y′, ′′, y′′ в точках x₁ = 0 и x₂ = 0,05.

k	x	y	∆y	∆2y	∆3y
0	0	1	0,221	0,059	0,011
1	0,1	1,221	0,270	0,060
2	0,2	1,491	0,330
3	0,3	1,822

□Составим таблицу конечных разностей: Находим для точки x₁ = 0:

u₁ =  = 0.

По формулам (1.24) получаем:

                      1 ⎛             1             1          ⎞

y′(0) =  _⎜0.221− 0.059 + 0.011_⎟ =1.952

                    0.1⎝             2             3          ⎠

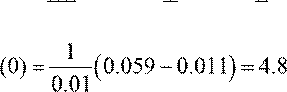y′′ y′′′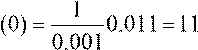

Для  точки  x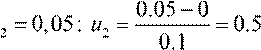, тогда по формулам (1.23) имеем:

1  ⎛ 2 0.5⋅ −1     3 0.5⋅ ² − 6 0.5⋅     + 2    ⎞

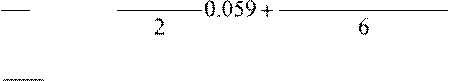y′(0,05) =  _⎜0.221+                                                         0.011_⎟ = 2.205;

0.1⎝⎠

y′′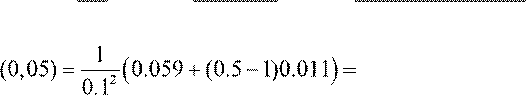                   5.35;                                                                    

y′′′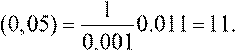

Здесь исходные данные получены для функции y = e^2x , поэтому точные значения производных можно сосчитать: y′(0) = 2, y′′(0) = 4, y′′′(0) =8; y′(0.05) = 2.210, y′′(0,05) = 4.421, y′′′(0,05) = 8.841.

Видим, что погрешности увеличиваются с ростом порядка производной и удалением от нулевого узла.

2  Приближенное вычисление определенного интеграла

2.1. Постановка задачи

b

  Основой всех способов вычисления определённого интеграла ∫ f ( )x dx

a  является свойство его аддитивности. Интеграл по промежутку интегрирования [a b, ] рассматривается как сумма интегралов по частичным промежуткам

[x_i,x_i+1], где i = 0,1,...,n −1, т.е.

b  n−1 n−1 ^xi+1

                                      I ⁼ ∫ f x dx( ) ⁼ ∑I_i ⁼ ∑ ∫ f x dx( )                                                .                       (2.1)

                                                                     a                                i=0                 i=0 x_i

Задача состоит в выборе достаточного числа разбиений отрезка [a b, ] (отрезки

[x_i,x_i+1], как правило, выбираются одинаковыми), и удачной замене подынтегральной функции f ( )x . Обычно она заменяется интерполяционным многочленом степени m:

f ( )x = P_m( )x + R x( ), (2.2) где R( )x – остаточный член интерполяции.

          Таким образом, на каждом частичном промежутке

                                                                     xi+1                                 xi+1

                                     I_i = ∫ P_m( )x dx + ∫ R( )x dx = I_i + S_i ,

                                                                       xi                                     xi

где I_i – приближённое значение интеграла на частичном промежутке, а S_i –

величина ошибки на том же промежутке.           Соответственно, приближённое значение интеграла
n−1 xi+1                                                     I = ∑ ∫ Pm( )x dx, i=0 xi	(2.3)

а ошибка

i n= −1^xi+1

                                                                                        S = ∑ ∫ R( )x dx.                     (2.4)

                                                                                                     i=0     xi

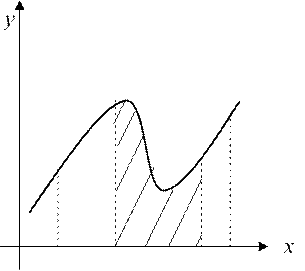
  На      рис.2.1         представлена геометрическая   интерпретация определённого интеграла, как площади криволинейной трапеции, ограниченной осью ОХ , графиком функции и прямыми x = a x,     = b, и интеграла I_i на частичном

0              a = x0 xi−1 xi b x= n                промежутке        [x_i−1,x_i ]                (заштрихованная

криволинейная трапеция).

Рис. 2.1. Геометрическая интерпретация определённого интеграла

Рассмотрим методы, использующие аппроксимацию подынтегральной функции многочленами нулевой ( f ( )x ≈ P x₀( ) = A₀ ), первой

( f ( )x ≈ P x₁( ) = A x₀ + A₁) и второй ( f ( )x ≈ P x₂( ) = A x₀ ² + A x₁ + A₂ ) степени. Для последующего вывода квадратурных формул и вычисления погрешностей нам потребуются теорема и лемма.

           Теорема (обобщённая теорема о среднем):

Пусть 1) функции f ( )x и g x( ) интегрируемы в интервале [a b, ];

2)  ∃m M, ∈ℜ:∀x∈[a b, ] m ≤ f (x) ≤ M , т.е. функция f ( )x ограничена на интервале [a b, ];

3)  функция      g x( ) знакопостоянна для любого     x из рассматриваемого интервала, т.е. ∀x∈[a b, ] g x( ) ≥ 0∨ g x( ) ≤ 0, тогда 

                                                                       b                                                    b

                                           ∫ f ( ) ( )x g x dx =µ∫ g x dx( )                                                                 ,                 (2.5)

                                                                       a                                                    a

где m ≤µ≤ M .

Лемма: пусть f ( )x непрерывна на [a b, ] и ξ_i ∈[a b, ] – произвольные точки, i =1,2,...,n . Тогда существует точка ξ∈[a b, ], такая, что f (ξ¹) + f (ξ²) +...+ f (ξⁿ)

                                                                                 = f ( )ξ .               (2.6)

n

          2.2. Метод прямоугольников

Разбиваем промежуток [a b, ] на n равных частей с шагом интегрирования h = (b − a)n.

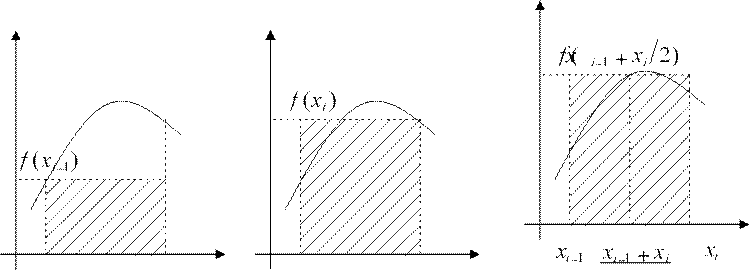
На каждом частичном промежутке  f ( )x заменяем многочленом нулевой степени f ( )x ≈ P x₀ ( )= A₀ . За A₀ можно принять любое значение f ( )x из интервала [x_i−1,x_i ]. Обычно за A₀ принимают значение f ( )x или в начале интервала, или в конце, или в середине. В зависимости от этого получают формулы левых, правых или средних прямоугольников.

                xi−1                     xi                     xi−1                     xi                                       2

                                  а)                                                б)                                       в)

Рис. 2.2. Метод прямоугольников: а) левых, б) правых, в) средних.

2.2.1. Формула левых прямоугольников  Запишем x_i и x_i+1 в виде 

                                             x_i = a + ih,  x_i+1 = a + (i +1)h                   (2.7)

                                    a+ +( 1)i h

и рассмотрим ∫ f ( )x dx . Разложим подынтегральную функцию f ( )x по

a ih+

формуле Тейлора в точке a + ih:

f ( )x = f a( + ih) + f ′(ξ_i )(x − a −ih), где ξ_i ∈[x_i,x_i+1]. Тогда a+ +( 1)i h a+ +( 1)i h

∫ f ( )x dx = ∫ [ f (a + ih) + f ′(ξ_i )(x − a −ih)]dx = f (a + ih)h +

                        a ih+                             a ih+

                        a+ +( 1)i h

                       +   f ′(ξ_i ( ))(x x − a −ih dx)        .

Используя обобщённую теорему о среднем, получим, что

                                                                                                                  a+ +( 1)i h

                                      a+ +( 1)i h f ′(ξi (x))(x − a −ih dx) =µi ∫ (x − a −ih dx)  =

                                           ∫                            a ih+                                       

2 2 a ih+a               i                   h

                                                     =µi                                            a ih=µi .

22

Если f ( )x непрерывна на [a b, ], то существует точка