Численные методы, теория функций комплексного переменного, дискретная математика. Интерполяция и численное дифференцирование

Тогда все слагаемые, кроме одного, не содержащего разности u − v v( = 0,1,...,k k, ≠ 0) будут равны нулю. И

                                                                                ⎧           k          1

⎪ω_k ( )u ^∑s=0 u − s, åñëè u ≠ v,

⎪

                                        ω′( )u = ⎨ k                                                                                        (1.20)

                                                                                ⎪∏(u − s),    åñëè   u = v,

⎪ s=0 ⎩ s v≠

v = 0,1,...,k k; ≠ 0.

          Полученные формулы позволяют вычислить приближённые значения производной при любом количестве узлов. В частности, при двух узлах интерполирования (линейная интерполяция)

1

                                                         f ′( )x = ∆y₀ .                             (1.21)

h

           При трёх узлах интерполирования (квадратичная интерполяция)

                                                               1 ⎡          2u −1   ^{2        ⎤                   1    2}

f ′( )x = _⎢∆y₀ + ₂ ∆ y_0⎦⎥, f ′′( )x = _h2 ∆ y₀ . (1.22) _{h ⎣}

При наличии четырёх узлов интерполирования формулы для производных примут вид:

                                                              1 ⎡          2u −1   ₂              3u² − 6u + 2   ₃        ⎤

f ′( )x =        ⎢∆y₀ +       ∆ y₀ +         ∆ y₀⎥, h ⎣         2        6        ⎦

1      ^{2                  3}         f ′′( )x =       2 ⎡_⎣∆ y₀ + (u −1)∆ y₀⎤_⎦,             (1.23)

_h

                                                                 1    ³

                                           f ′′′( )x = ₃ ∆ y₀.

h

Если производная вычисляется в нулевом узле, то u = 0 и формулы (1.23) приобретают вид:

                                                                                 1⎛          1   2               1   3        ⎞

f ′( )x =       ⎜∆y0 −       ∆ y0 +       ∆ y0 ⎟, h⎝       2        3       ⎠

1    ^{2                  3}         f ′′( )x =       ₂ (∆ y₀ − ∆ y₀ ),               (1.24)

h

                                                                                  1    ³

                                                             f ′′′( )x = ₃ ∆ y₀.

h

Ошибка при вычислении производных существенно увеличивается при увеличении порядка производной, поэтому обычно для вычисления производных порядка выше третьего этот метод не используется.

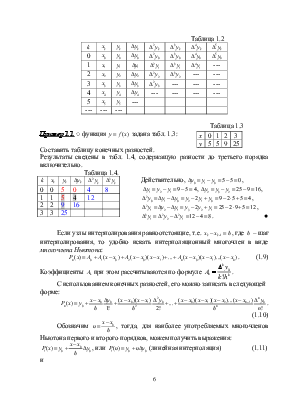
 Пример 1.2. Функция задана табл. 1.5.                                      Таблица 1.5.

Вычислить производные y y′, ′′, y′′ в точках x₁ = 0 и x₂ = 0,05.

□Составим таблицу конечных разностей: Находим для точки x₁ = 0:

u₁ =  = 0.

По формулам (1.24) получаем:

                      1 ⎛             1             1          ⎞

y′(0) =  _⎜0.221− 0.059 + 0.011_⎟ =1.952

                    0.1⎝             2             3          ⎠

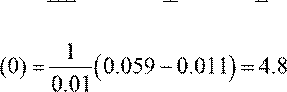y′′ y′′′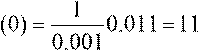

Для  точки  x, тогда по формулам (1.23) имеем:

1  ⎛ 2 0.5⋅ −1     3 0.5⋅ ² − 6 0.5⋅     + 2    ⎞

y′(0,05) =  _⎜0.221+                                                         0.011_⎟ = 2.205;

0.1⎝⎠

y′′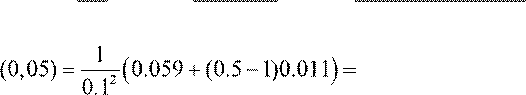                   5.35;                                                                    

y′′′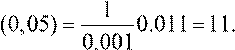

Здесь исходные данные получены для функции y = e^2x , поэтому точные значения производных можно сосчитать: y′(0) = 2, y′′(0) = 4, y′′′(0) =8; y′(0.05) = 2.210, y′′(0,05) = 4.421, y′′′(0,05) = 8.841.

Видим, что погрешности увеличиваются с ростом порядка производной и удалением от нулевого узла.

2  Приближенное вычисление определенного интеграла

2.1. Постановка задачи

b

  Основой всех способов вычисления определённого интеграла ∫ f ( )x dx

a  является свойство его аддитивности. Интеграл по промежутку интегрирования [a b, ] рассматривается как сумма интегралов по частичным промежуткам

[x_i,x_i+1], где i = 0,1,...,n −1, т.е.

b  n−1 n−1 ^xi+1

                                      I ⁼ ∫ f x dx( ) ⁼ ∑I_i ⁼ ∑ ∫ f x dx( )                                                .                       (2.1)

                                                                     a                                i=0                 i=0 x_i

Задача состоит в выборе достаточного числа разбиений отрезка [a b, ] (отрезки

[x_i,x_i+1], как правило, выбираются одинаковыми), и удачной замене подынтегральной функции f ( )x . Обычно она заменяется интерполяционным многочленом степени m:

f ( )x = P_m( )x + R x( ), (2.2) где R( )x – остаточный член интерполяции.

          Таким образом, на каждом частичном промежутке

                                                                     xi+1                                 xi+1

                                     I_i = ∫ P_m( )x dx + ∫ R( )x dx = I_i + S_i ,

                                                                       xi                                     xi

где I_i – приближённое значение интеграла на частичном промежутке, а S_i –

а ошибка

i n= −1^xi+1

                                                                                        S = ∑ ∫ R( )x dx.                     (2.4)

                                                                                                     i=0     xi

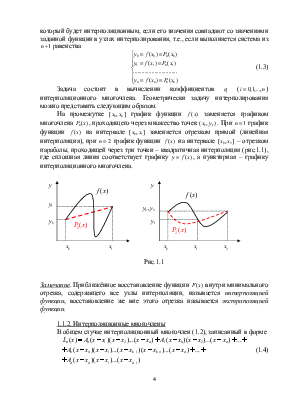
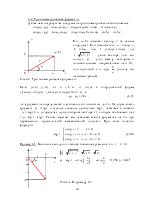
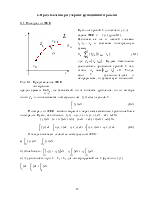
  На      рис.2.1         представлена геометрическая   интерпретация определённого интеграла, как площади криволинейной трапеции, ограниченной осью ОХ , графиком функции и прямыми x = a x,     = b, и интеграла I_i на частичном

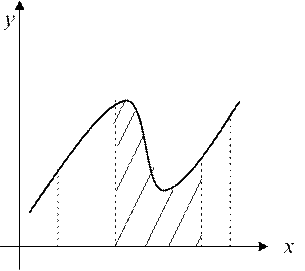0              a = x0 xi−1 xi b x= n                промежутке        [x_i−1,x_i ]                (заштрихованная

криволинейная трапеция).

Рис. 2.1. Геометрическая интерпретация определённого интеграла

Рассмотрим методы, использующие аппроксимацию подынтегральной функции многочленами нулевой ( f ( )x ≈ P x₀( ) = A₀ ), первой

( f ( )x ≈ P x₁( ) = A x₀ + A₁) и второй ( f ( )x ≈ P x₂( ) = A x₀ ² + A x₁ + A₂ ) степени. Для последующего вывода квадратурных формул и вычисления погрешностей нам потребуются теорема и лемма.

           Теорема (обобщённая теорема о среднем):

Пусть 1) функции f ( )x и g x( ) интегрируемы в интервале [a b, ];

2)  ∃m M, ∈ℜ:∀x∈[a b, ] m ≤ f (x) ≤ M , т.е. функция f ( )x ограничена на интервале [a b, ];

3)  функция      g x( ) знакопостоянна для любого     x из рассматриваемого интервала, т.е. ∀x∈[a b, ] g x( ) ≥ 0∨ g x( ) ≤ 0, тогда 

                                                                       b                                                    b

                                           ∫ f ( ) ( )x g x dx =µ∫ g x dx( )                                                                 ,                 (2.5)

                                                                       a                                                    a

где m ≤µ≤ M .

Лемма: пусть f ( )x непрерывна на [a b, ] и ξ_i ∈[a b, ] – произвольные точки, i =1,2,...,n . Тогда существует точка ξ∈[a b, ], такая, что f (ξ¹) + f (ξ²) +...+ f (ξⁿ)

                                                                                 = f ( )ξ .               (2.6)

n

          2.2. Метод прямоугольников

Разбиваем промежуток [a b, ] на n равных частей с шагом интегрирования h = (b − a)n.

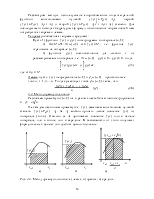
На каждом частичном промежутке  f ( )x заменяем многочленом нулевой степени f ( )x ≈ P x₀ ( )= A₀ . За A₀ можно принять любое значение f ( )x из интервала [x_i−1,x_i ]. Обычно за A₀ принимают значение f ( )x или в начале интервала, или в конце, или в середине. В зависимости от этого получают формулы левых, правых или средних прямоугольников.

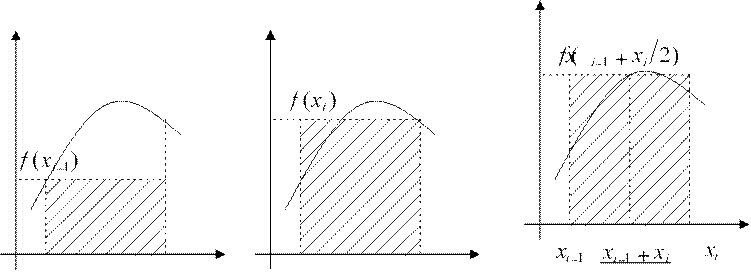
                xi−1                     xi                     xi−1                     xi                                       2

                                  а)                                                б)                                       в)

Рис. 2.2. Метод прямоугольников: а) левых, б) правых, в) средних.

2.2.1. Формула левых прямоугольников  Запишем x_i и x_i+1 в виде 

                                             x_i = a + ih,  x_i+1 = a + (i +1)h                   (2.7)

                                    a+ +( 1)i h

и рассмотрим ∫ f ( )x dx . Разложим подынтегральную функцию f ( )x по

a ih+

формуле Тейлора в точке a + ih:

f ( )x = f a( + ih) + f ′(ξ_i )(x − a −ih), где ξ_i ∈[x_i,x_i+1]. Тогда a+ +( 1)i h a+ +( 1)i h

∫ f ( )x dx = ∫ [ f (a + ih) + f ′(ξ_i )(x − a −ih)]dx = f (a + ih)h +

                        a ih+                             a ih+

                        a+ +( 1)i h

                       +   f ′(ξ_i ( ))(x x − a −ih dx)        .

Используя обобщённую теорему о среднем, получим, что

                                                                                                                  a+ +( 1)i h

                                      a+ +( 1)i h f ′(ξi (x))(x − a −ih dx) =µi ∫ (x − a −ih dx)  =

                                           ∫                            a ih+                                       

2 2 a ih+a               i                   h

                                                     =µi                                            a ih=µi .

22

Если f ( )x непрерывна на [a b, ], то существует точка