Методы оптимизации. Расчет оптимального выпуска продукции

МИНИСТЕРСТВО  ОБРАЗОВАНИЯ  РОССИЙСКОЙ  ФЕДЕРАЦИИ

Северо-Западный государственный заочный технический университет

Кафедра информатики и прикладной математики

Лабораторная работа

по дисциплине «математика»

Тема: Методы оптимизации.

Выполнил студент Саркисян Николай Александрович

Институт: ИУП и ИП

Курс 2

Специальность: 080507.65

Шифр: 8703031173

Руководитель:_____________________

Дата защиты:_____________________

Оценка:_____________________

Подпись преподавателя:_____________________

Санкт-Петербург

2010

Содержание

1. Распределение ресурсов………………………………………………………..3

1.1. Графическое решение…………………………………………………..……3

1.2. Решение симплекс-методом……………………………………………..…..6

1.3.Решение в Excel - поиск решения………………………………………….10

2. Транспортная задача……………………………………………………….…13

2.1. Решение в Excel - поиск решения……………………………………….....13

2.2. Решение методом потенциалов…………………………………………….16

Задание 1: Распределение ресурсов.

Вариант 3

Фирма выпускает два вида изделий A и B. Каждое изделие проходит обработку на двух технологических линиях. Известны технологические коэффициенты времени обработки (в минутах) каждого изделия на каждой технологической линии. Кроме этого, известны рыночная цена каждого изделия и общее время работы каждой линии. Найти оптимальный выпуск продукции.

	А	В	Общее время
Линия 1	60	23	1380
Линия 2	33	60	1980
Цена изделия	20	15

1.1: Графическое решение

Стандартная форма: x1-выпуск А, x2-выпуск В

Zmax=max(20*x1+15*x2)

ограничения: 60*x1+23*x2<=1380

33*x1+60*x2<=1980

x1>=0, x2>=0

Каноническая форма: Zmax=max(20*x1+15*x2+0*s1+0*s2)

ограничения: 60*x1+23*x2+s1=1380

33*x1+60*x2+s2=1980

x1>=0, x2>=0, s1>=0, s2>=0

Найдём базисные ограничения

x1, x2 - свободные переменные

x1=0, x2=0, s1=1380, s2=1980 - является допустимым

Z=20*x1+15*x2=0

x1, s1 - свободные переменные

23*x2=1380

60*x2+s2=1980

x1=0, x2=60, s1=0, s2=-1620 - не является допустимым

x1, s2 - свободные переменные

23*x2+s1=1380

60*x2=1980

x1=0, x2=33, s1=621, s2=0 - является допустимым

Z=15*x2=495

x2, s1 - свободные переменные

60*x1=1380

33*x1+s2=1980

x1=23, x2=0, s1=0, s2=1221 - является допустимым

Z=20*x1=460

x2, s2 - свободные переменные

60*x1+s1=1380

33*x1=1980

x1=60, x2=0, s1=-2220, s2=0 - не является допустимым

s1, s2 - свободные переменные

60*x1+23*x2=1380

33*x1+60*x2=1980

x1=13,1151, x2=25,7867, s1=0, s2=0 - является допустимым

Z=20*x1+15*x2=649,1024

№	Базисные переменные		Небазисные переменные		Z
1	s1=1380	s2=1980	x1=0	x2=0	0
2	x2=33	s1=621	x1=0	s2=0	459
3	x1=23	s2=1221	x2=0	s1=0	460
4	x1=13,1151	x2=25,7867	s1=0	s2=0	649,1024

Максимальная выручка: 649,1024 у.е. - № 4 номер в таблице

60*x1+23*x2<=1380

x2=0, A(23,0)

x1=0, B(0,60)

33*x1+60*x2<=1980

x2=0, C(60,0)

x1=0, D(0,33)

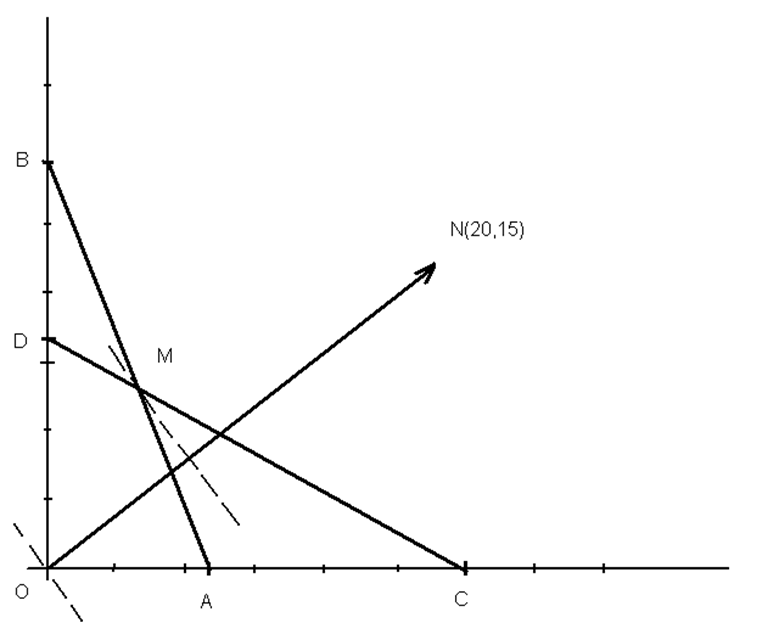
Таким образом, точка Mопределяет оптимальное решение.

Соответствующее точке Mбазисное решение

X*={x1=13,1151, x2=25,7867, s1 =0, s2 =0}

является оптимальным решением.

Максимальная выручка будет равна:

Z* =649,1024

Уравнение: 20*x1+15*x2=649,1024

Максимальная выручка Z* =649,1024 у.е достигается при производстве продукции А=13,1151 ед. и продукции В=25,7867 ед., при этом обе линии заняты полностью.

1.2: Решение симплекс-методом

Построение начального базисного плана

Пусть в начальном базисном плане x1, x2 – свободные переменные

(x1= x2=0), а s1 =1380 и s2=1980 базисные переменные.

Решение в Excel:

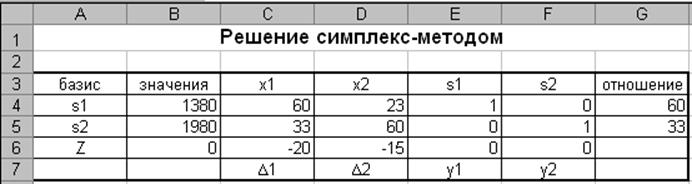
В ячейки В4:В5 введем числовые значения 1380 и 1980 базисных переменных s1 и s2. Остальные столбцы состоят из коэффициентов перед переменными xj в левых частях ограничений.

Последняя строка симплекс-таблицы состоит из значений целевой функции Z = 0 и коэффициентов целевой функции Z.

Итерация 1

Значения, расположенные в последней строке симплекс-таблицы в столбцах переменных x1 и x2 отрицательны - таблица не определяет оптимального плана.

Выберем x2 в качестве новой базисной переменной.

Определяем новую свободную переменную: В ячейку G4 введем формулу =B4/D4 в ячейку G5 введем формулу =B5/D5.

Минимальное значение в ячейке G5, базисная переменная s2 переходит в свободные.

Составим таблицу для нового базиса s1, x2

В ячейку B12 введем формулу =B5/$D5$ и скопируем  в C12:F12.

B ячейку В11 введем формулу =B4-B5*$D$4/$D$5 и скопируем в C11:F11.

B ячейку В13 введем формулу=B6-B5*$D$6/$D$5 и скопируем в C13:F13.

В результате пересчета получили новую симплекс-таблицу.

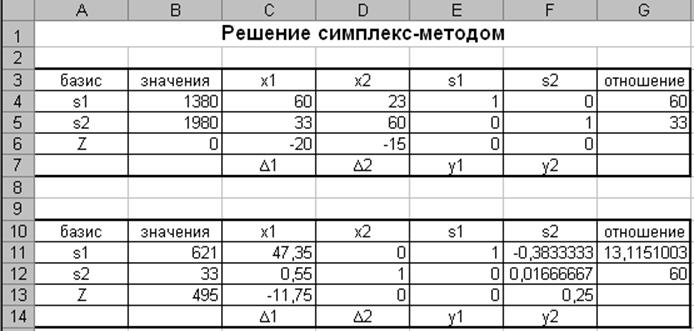
Итерация 2

Значение в последней строке симплекс-таблицы в столбце переменной x1, отрицательно – таблица не определяет оптимального плана.

Переменную x1 вводим в базис.

В ячейку G11 введем формулу =B11/С11 и скопируем в ячейку G12

Минимальное значение в ячейке G11 базисная переменная s1 переходит в свободные.

x1 и x2 – базисные переменные, а s1, s2 – свободные переменные.

Составим таблицу для нового базиса x1, x2

В ячейку B18 введем формулу =B11/$C$11 и скопируем  в C18:F18.

B ячейку В19 введем формулу =B12-B11*$C$12/$C$11 и скопируем в C19:F19.

B ячейку В20 введем формулу =B13-B11*$C$13/$C$11 и скопируем в C20:F20.

В результате пересчета получили новую симплекс-таблицу.

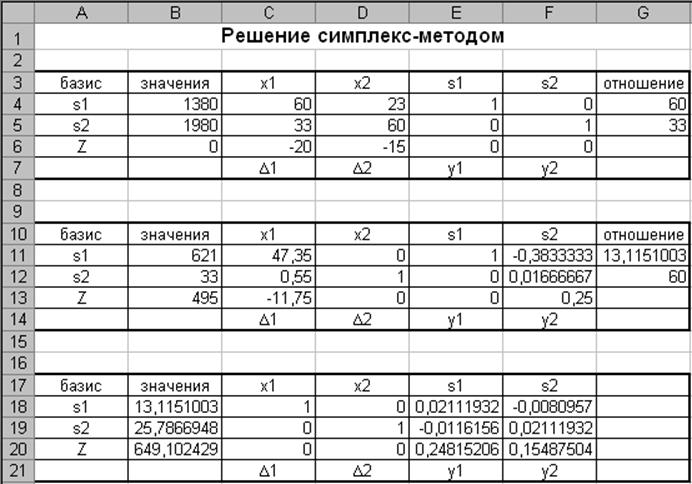
Итерация 3

Среди значений последней строки симплекс-таблицы нет отрицательных, эта таблица определяет оптимальные планы прямой и двойственной задач.

Анализ оптимальной симплекс-таблицы

Значения во втором столбце определяют базисные переменные x1 = 13,1151, x2 = 25,7867

Все переменные, не входящие в первый столбец, являются свободными