Методы оптимизации. Расчет оптимального выпуска продукции, страница 2

и поэтому равны 0: s1=0, s2=0.

Значение целевой функции прямой задачи

Z = 649,1024 у.е. (в ячейке B20).

Таким образом, оптимальный план прямой задачи

X*={x1=13,1151, x2=25,7867, s1=0, s2 = 0}:

Продукт А производится в количестве 13,1151 единиц, продукт В производится в количестве 25,7867 единиц, обе линии производства заняты полностью.

В последней строке симплекс-таблицы значения 0 в столбцах x1 и x2

означают, что производства первого и второго продуктов рентабельны: ∆1=0, ∆2=0.

Значение 0,2481 в столбце s1 означает, что теневая цена работы 1 линии оборудования равна 0,2481, значение 0,1549 в столбце s2 означает, что теневая цена работы 2 линии оборудования равна 0,1549.

Оптимальное решение двойственной задачи:

Y* = {y1=0,2481, y2=0,1549, Δ1=0, Δ2=0}.

Отображение симплекс-таблиц с формулами:

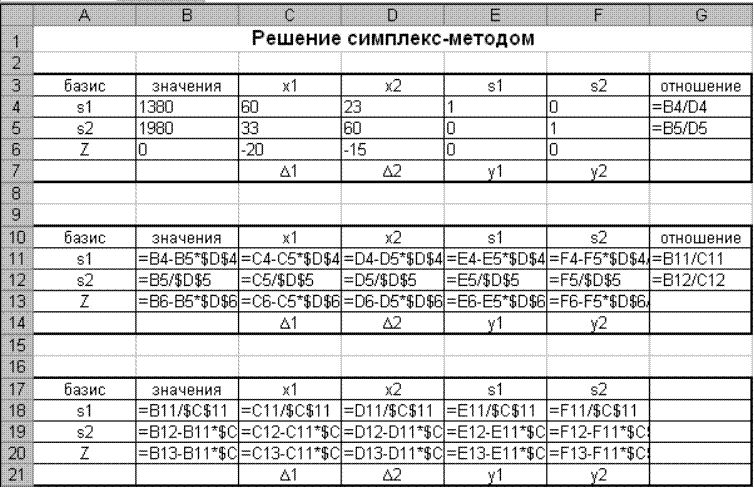
1.3: Решение в Excel- поиск решения

	А	В	Общее время
Линия 1	60	23	1380
Линия 2	33	60	1980
Цена изделия	20	15

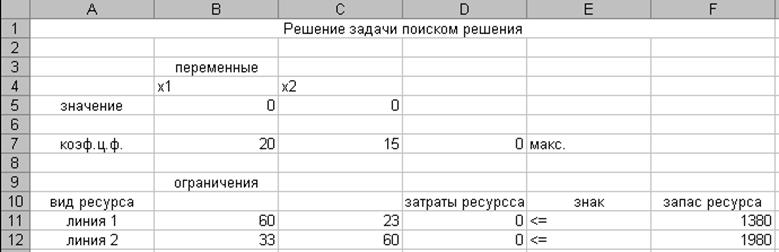
В электронную таблицу вносим исходные данные:

В ячейки B7:C7 – коэффициенты целевой функции, стоимость изделий

В ячейки B11:C12 – нормы затрат времени на каждый вид продукции

В ячейки F11:F12 –  максимальное время работы линий

В ячейку D7 (целевая ячейка) вносим формулу для вычисления выручки =СУММПРОИЗВ($B$5:$C$5;B7:C7)

Содержимое ячейки D7 копируем в ячейки D11: D12

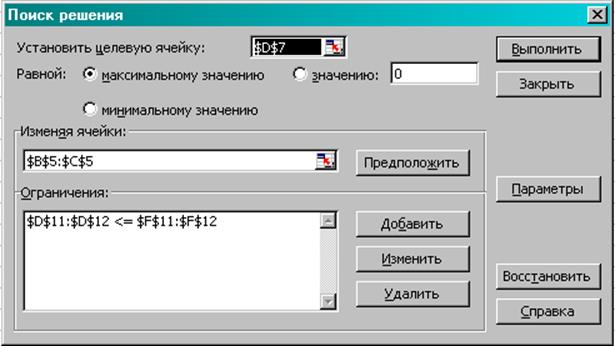
В диалоговом окне Поиск решения:

Целевая ячейка $D$7

Изменяя ячейки $B$5:$C$5

Ограничения $D$11:$D$12<=$F$11:$F$12

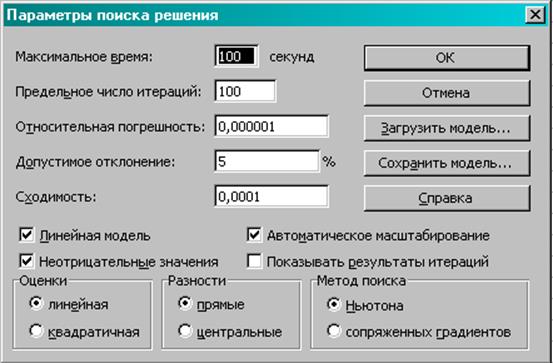
В окне Поиск решения нажать кнопку Параметры и в появившемся окне заполнить окна параметров, нажать кнопку ОК.

В окне Поиск решения нажать кнопку Выполнить для запуска режима

Поиск решения и нажать кнопку ОК.

Выбрать Сохранить найденное решение нажать OК

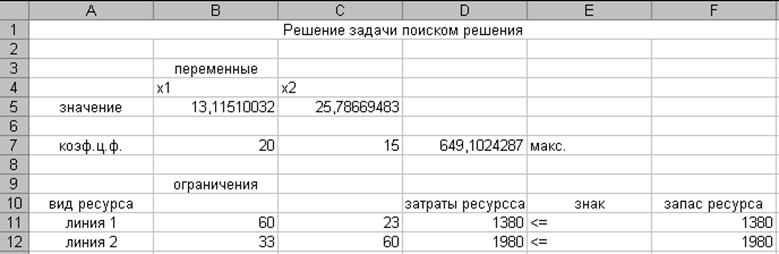
В ячейке D7 максимальная выручка 649,1024 у.е. при выпуске продукции А и В в ячейках В5:С5: А=13,1151 ед., В=25,7867ед.

Задание 2: Транспортная задача

Вариант 3

В трех пунктах производства: A1, A2, A3 изготавливается однородная продукция в количествах: a1=300, a2=440, a3=270 соответственно.

Эту продукцию требуется доставить в четыре пункта потребления: B1, B2, B3, В4 в количествах b1=270, b2=330, b3=310, b4=100 соответственно.

Матрица стоимостей перевозок единицы продукции cijиз пункта производства Ai в пункт потребления Bj:

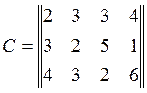
Требуется определить план перевозок, который минимизирует транспортные расходы.

2.1: Решение в Excel- поиск решения

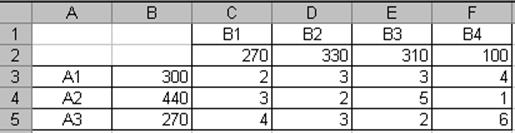
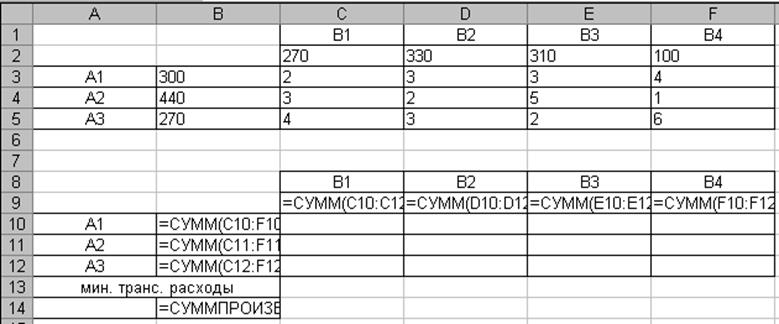
Заполнение исходных данных

В ячейках B3:B5 помещены максимальные объемы производства, в ячейках

C2:F2 помещены минимальные объемы потребления, в ячейках C3:F5 помещены стоимости перевозок.

Внесение формул

В ячейки B10:B12 внесем формулы, вычисляющие левые части ограничений:

в ячейку B10 введем формулу для вычисления количества продукции, вывозимой из пункта А1 =СУММ(C10:F10); для вычисления количества продукции, вывозимой из пунктов А2 и А3 скопируем формулу в ячейке B10 в ячейки B11 и B12.

В ячейки C9:F9 внесем формулы, вычисляющие левые части ограничений:

в ячейку C9 введем формулу, вычисляющую количество продукции, необходимое в пункте потребления В1 =СУММ(C10:C12); для вычисления количества продукции, необходимой в пунктах В2, В3 скопируем формулу в ячейке С9 в ячейки D9:F9.

В целевую ячейку B14 внесем формулу для целевой функции =СУММПРОИЗВ(C3:F5;C10:F12)

Заполнение окна Поиск решения.

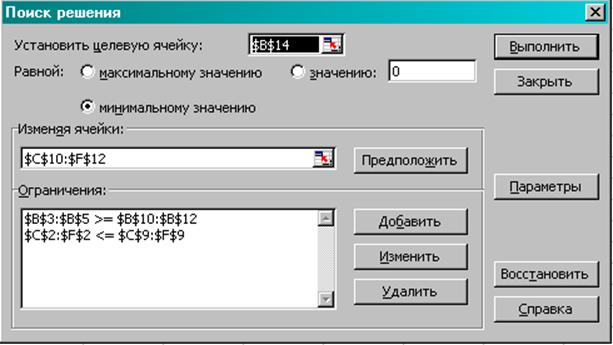
В диалоговом окне Поиск решения:

Целевая ячейка $B$14

Изменяя ячейки $C$10:$F$12

Ограничения $B$3:$B$5>=$B$10:$B$12, $C$2:$F$2<=$C$9:$F$9

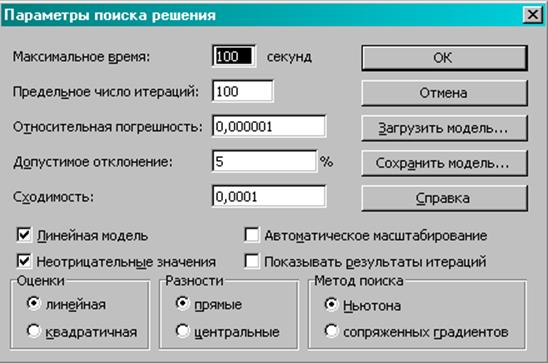
В окне Поиск решения нажать кнопку Параметры и в появившемся окне заполнить окна параметров, нажать кнопку ОК.

В окне Поиск решения нажать кнопку Выполнить для запуска режима

Поиск решения и нажать кнопку ОК.

Выбрать Сохранить найденное решение нажать OК

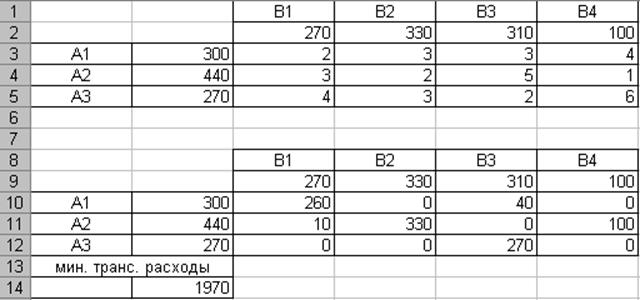
В ячейках C10:F12 оптимальный план перевозок:

x11=260, x12=0, x13=40, x14=0, x21=10, x22=330, x23=0, x24=100, x31=0, x32=0, x33=270, x34=0.

В ячейке B15 минимальные транспортные расходы: 1970 у.е.

2.2: Решение методом потенциалов

Суммарный запас продукции А=300+440+270=1010  равен суммарному заказу В=270+330+310+100=1010 – следовательно задача закрытая

Составим начальный план методом наименьшей стоимости:

	B1=270 V=2	B2=330 V=0	B3=310 V=3	B4=100 V=-1
A1=300 U=0	2 270 -	3 3	3 30 +	4 5
A2=440 U=2	3   -1                 +	2 330	5 10 -	1 100
A3=270 U=-1	4 3	3 4	2 270	6 8

n+m-1=6, базисных клеток 6 – план невырожденный

Вводим потенциалы U и V для базисных клеток, так что C=U+V

Для свободных клеток вычислим разность ∆С=C-(U+V)

∆С2.1=-1<0 – план не оптимален,  строим цикл С2.1-С2.3-С1.3-С1.1 ∆X=min(270,10)=10

Исследуем новый план:

	B1=270 V=1	B2=330 V=0	B3=310 V=2	B4=100 V=-1
A1=300 U=1	2 260	3 2	3 40	4 4
A2=440 U=2	3 10	2 330	5 1	1 100
A3=270 U=0	4 3	3 3	2 270	6 7

n+m-1=6, базисных клеток 6 – план невырожденный

Вводим потенциалы U и V для базисных клеток, так что C=U+V

Для свободных клеток вычислим разность ∆С=C-(U+V)

∆С>=0 – план оптимален

x11=260, x12=0, x13=40, x14=0, x21=10, x22=330, x23=0, x24=100, x31=0, x32=0, x33=270, x34=0.

Минимальные транспортныерасходы

Zmin=260*2+40*3+10*3+330*2+100*1+270*2=1970 у.е.