Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Р.Е. Алексеева
Кафедра «Прикладная математика»
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
Методическое пособие
Нижний Новгород 2011
Составители: С.Н. ,
УДК 517
Поверхностные интегралы. Методическое пособие / С. Н. , Л.Ю. . НГТУ, Н. Новгород, 2011 - 30с.
Методическое пособие содержит изложение лекционного материала по разделу «Поверхностные интегралы». Приведены задачи на вычисление поверхностных интегралов первого и второго типов, предназначенные для выполнения индивидуальных типовых расчётов.
Подписано в печать . Формат 60х84 1/16. Бумага газетная.
Печать офсетная. Усл. п. л. . Уч.-изд. л. . Тираж 300 экз. Заказ .
Нижегородский государственный технический университет.
Типография НГТУ.603950, Нижний Новгород, ул.Минина, 24.
© ,
©Нижегородский государственныйтехнический университет им. Р.Е. Алексеева, 2011
Тема «Поверхностные интегралы» представляет собой один из наиболее сложных разделов, изучаемых в рамках курса «Математический анализ». Эта сложность обусловлена двумя причинами: сами поверхностные интегралы являются довольно сложными математическими понятиями, для хорошего усвоения которых требуется немало времени, выделить достаточное количество времени для её подробного изучения в рамках лекционного курса никогда не удаётся.
Проблема нехватки времени наложила свой отпечаток на изложение материала во всех известных учебниках, исключая «Курс дифференциального и интегрального исчисления» Г. М. Фихтенгольца в трех томах. Во всех учебниках разделы, входящие в первую половину курса «Математический анализ», такие как «Пределы», «Производная» «Неопределенный и определенный интеграл», «Ряды» и т.п., изложены методически примерно одинаково и, в общем, отличаются лишь второстепенными деталями. Но тема «Поверхностные интегралы» в различных учебниках излагается по-разному. Изложение материала отличается не только полнотой, но и последовательностью введения основных понятий и их взаимозависимостью друг от друга.
В предлагаемом методическом пособии весь учебный материал по поверхностным интегралам изложен последовательно и с достаточной полнотой, чтобы им можно было уверенно пользоваться. В принципиальном плане изложение материала соответствует «Курсу дифференциального и интегрального исчисления» Г. М. Фихтенгольца. Однако, за счет того, что материал дан не в такой общности, как в вышеупомянутой книге, его объём удалось значительно сократить, а доказательства упростить. Материал расположен так, чтобы доказательства были не слишком длинными.Данное учебное пособие включает ряд параграфов, обычно изучаемых в предыдущих разделах курса математического анализа. К ним относятся: «Определение компонент вектора, направленного по касательной», «Определение направляющих косинусов нормали» и «Формула Грина».
Весь материал рассчитан на изложение в пределах 4-х лекций и содержит по 16 задач на вычисление поверхностных интегралов первого и второго типов, предназначенных для выполнения индивидуальных типовых расчётов.
Рассмотрим
в трёхмерном пространстве с декартовой системой координат ![]() некоторую
кривую
некоторую
кривую ![]() , заданную
параметрическими уравнениями
, заданную
параметрическими уравнениями
![]() ,
, ![]() ,
, ![]() ,
, ![]() . (1)
. (1)
Выясним, как имея уравнение (1), определить компоненты вектора касательной к кривой. По своему определению, касательная – это предельное положение секущей.
|
Рис. 1. |
Пусть |
Возьмём приращение
![]() параметра
параметра
![]() , тогда
, тогда![]() .Вектор
.Вектор![]() представляет
собой секущую кривой
представляет
собой секущую кривой ![]() .
Рассмотрим отношение
.
Рассмотрим отношение![]() . Это
вектор, коллинеарный с вектором
. Это
вектор, коллинеарный с вектором ![]() , так как
получается из него умножением на скалярный множитель
, так как
получается из него умножением на скалярный множитель ![]() . Можно
записать этот вектор так:
. Можно
записать этот вектор так:
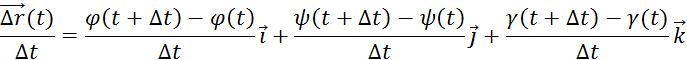
Если функции ![]() ,
, ![]() и
и ![]() дифференцируемы,
то:
дифференцируемы,
то:![]() .Вектор,
определяемый последним равенством, называется производной от вектора
.Вектор,
определяемый последним равенством, называется производной от вектора![]() по
скалярному аргументу
по
скалярному аргументу ![]() .
Производную обозначают символом
.
Производную обозначают символом ![]() . Таким
образом
. Таким
образом
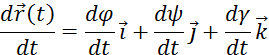
Выясним
направление вектора![]() .Так как
при
.Так как
при ![]() , точка
, точка ![]() приближается
к точке
приближается
к точке ![]() , то
направление секущей
, то
направление секущей ![]() в пределе
даёт направление касательной. Следовательно, вектор производной
в пределе
даёт направление касательной. Следовательно, вектор производной ![]() направлен
по касательной к кривой
направлен
по касательной к кривой ![]() в точке
в точке ![]() .
Компоненты вектора
.
Компоненты вектора ![]() ,
направленные по касательной, равны:
,
направленные по касательной, равны:![]() , а его
длина определяется формулой:
, а его
длина определяется формулой:![]() .
.
Пусть
имеется поверхность, уравнение которой имеет вид ![]() ,
, ![]() -
произвольная точка на заданной поверхности.Пересечём заданную поверхность
плоскостью, проходящей через заданную точку
-
произвольная точка на заданной поверхности.Пересечём заданную поверхность
плоскостью, проходящей через заданную точку ![]() параллельно
координатной плоскости
параллельно
координатной плоскости ![]() .Уравнение
такой плоскости имеет вид
.Уравнение
такой плоскости имеет вид![]() .
Пересечение поверхности
.
Пересечение поверхности![]() с
плоскостью
с
плоскостью ![]() даёт
некоторую кривую
даёт
некоторую кривую ![]() ,
параметрические уравнения которой имеют вид:
,
параметрические уравнения которой имеют вид: ![]() ,
, ![]() ,
, ![]() (здесь
(здесь ![]() -
параметр).Вектор, касательный к линии
-
параметр).Вектор, касательный к линии ![]() , будет
иметь вид
, будет
иметь вид ![]() .В точке
.В точке ![]() :
: ![]() .
.
Также
пересечём поверхность![]() плоскостью
плоскостью
![]() , через
точку
, через
точку ![]() параллельно
параллельно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.