Регрессионная модель работы прядильной машины, характеризующая зависимость средней обрывности от скорости вращения веретен

то факторы – это инвестиции, коэффициенты обновления оборудования, степень автоматизации и т.п., а в качестве отклика может выступать прибыль. Так как мы не исследуем процессов преобразования факторов в отклик, то и не можем сказать, какова теоретическая форма связи между ними. Поэтому зависимость между откликом и факторами находятся по МНК, т.е. в виде уравнения средней квадратической регрессии и называется регрессионной моделью. Регрессионные модели обычно имеют вид многочлена, если нет оснований для выбора другого вида зависимости, исходя из геометрического представления точек, соответствующих результатам экспериментов (например, наличие разрывов, асимптот или периодичности).

Пример 11. Исследовалась прядильная машина (лабораторная прядильная установка) в целях определения влияния частоты вращения веретен на величину обрывности. Фактор Х – частота вращения веретен в 1000 об./мин. менялся на четырех уровнях: 12,5; 13,7; 14,0 и 14,7. Обрывность измерялась числом обрывов за время наработки съема. Опыты проводились в 6-ти повторностях. Результаты статического анализа опытов приведены в табл. П12.

Замечание. Как уже говорилось выше, мы считаем, что значения факторов являются точными, а все случайные ошибки факторов отнесены к отклику. Поэтому под повторностью опыта мы понимаем не повторное измерение отклика, а именно полное повторение опыта, т.е. все – начиная от переналадки  и перезаправки оборудования до получения нового значения отклика. Рекомендуется провести первую повторность первого опыта (в нашем примере при Х = 12,5), затем перезаправить оборудование и провести первую повторность второго опыта (при Х = 13,7), а потом вернуться к первому опыту и провести его вторую повторность. Или можно провести все опыты по одному разу, потом все их повторить (получить вторые повторности) и т.д. Таким образом, колебания значений отклика (в нашем примере обрывности) будут связаны не только с его собственной случайностью, но и со случайными колебаниями факторов. 

Таблица П12

Регрессионная модель работы прядильной машины, характеризующая зависимость средней обрывности от скорости вращения веретен, была найдена МНК в виде многочлена второй степени

y = 502,9 – 76,35x + 2,93x²

Теперь возникает вопрос о соответствии модели объекту, т.е. об адекватности модели.

Так как отклик является случайной величиной и в результате проведенных экспериментов найдены оценки математического ожидания этой величины и ее дисперсии, то можно для каждого уровня фактора найти доверительный интервал с заданной надежностью g. Если границы доверительных интервалов для каждого значения Х нанести на график и соединить ломаной линией, то получится некая полоса. Любая функция y= f(x), лежащая внутри этой полосы, может быть призвана адекватной моделью. Для рассматриваемого примера были найдены границы доверительных интервалов по формуле

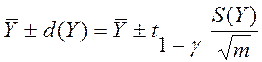                  (19.1)

где d(Y) – случайная ошибка оценки математического ожидания;

S(Y) – оценка среднего квадратического отклонения;

m – число повторностей каждого опыта;

t_1-g - параметр распределения Стьюдента с m – 1 степенью свободы и уровнем значимости 1 - g.

Для надежности g = 0,95 по таблицам распределения Стьюдента находим t_0,05 = 2,57. Результаты вычисления границ доверительных интервалов приведены в табл. П13.

Таблица П13

График на котором приведены границы доверительных интервалов и оценки средних значений из табл.П12, представлен на рис.5.

Для проверки адекватности модели используется следующее правило. По всем опытам определяется средняя дисперсия опыта

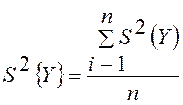,                              (19.2)

где n – число опытов (число уровней фактора).

Эта дисперсия имеет n(m – 1) степеней свободы.

По расчетным значениям отклика по уравнению регрессии Y^* определяется дисперсия адекватности по формуле