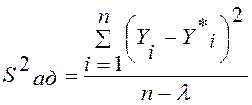Регрессионная модель работы прядильной машины, характеризующая зависимость средней обрывности от скорости вращения веретен, страница 2

,                           (19.3)

где l - число коэффициентов, определяемых по МНК.

Эта дисперсия имеет n - l степеней свободы.

По F – критерию Фишера проверяется значимость различия дисперсий опыта и адекватности, причем дисперсия адекватности всегда состоит в числителе, так как если F < 1, то модель адекватна. По числам степеней свободы числителя и знаменателя и по уровню значимости 1 - g по таблицам распределения Фишера определяется F_1-g , и тогда критерий адекватности определяется неравенством

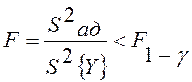                           (19.4)

Пример 11 (продолжение). Найдем дисперсию опыта по данным табл.П12

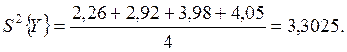
Для вычисления дисперсии адекватности составим табл.П14

Таблица П14

X	Y	Y*	(Y – Y*)2
12,5	6,33	6,34	0,0001
13,7	6,50	6,84	0,1156
14,0	8,31	8,28	0,0009
14,7	13,17	13,70	0,2809
Сумма			0,8109

Так как n = 4 и l = 3, то дисперсия адекватности (19.3)

S²_ад = 0,8109 и F<1,

Следовательно, модель в виде многочлена второй степени адекватна.

Если объектом исследования является работающее предприятие или проведение повторных опытов по каким-то причинам невозможно, то рассмотренный выше метод проверки адекватности модели не может быть использован. В этом случае следует найти коэффициент корреляции между расчетными Y^* и фактическими Y значениями отклика по формуле

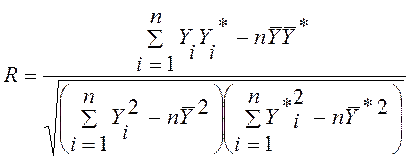,              (19.5)

где - средние значения фактических и расчетных значений отклика соответственно;

n – число опытов.

Значимость этого коэффициента корреляции определяется по формулам (16.2), (16.3), т.е. находится среднее квадратическое отклонение R по формуле

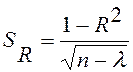,                   (19.6)

где l - число коэффициентов в модели.

По числе степеней свободы n -l и уровню значимости а  по таблицам распределения Стьюдента находим t_a , и тогда критерий значимости коэффициента корреляции R определяется неравенством

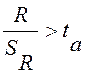                              (19.7)

Если коэффициент R значим, то модель адекватна. Возможность использовать коэффициент корреляции для проверки адекватности модели объясняется тем, что МНК не дает систематической ошибки и фактические и расчетные значения имеют одинаковую тенденцию.

Для построения регрессионных моделей с несколькими факторами их обычно кодируют с тем, чтобы избежать ошибок, связанных с различным порядком их значений. Кроме того, если факторы кодированы, то по значениям коэффициентов регрессии можно сравнить степень их влияния на отклик. Кодирование факторов производится по формуле

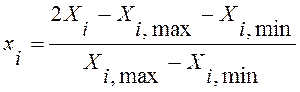                          (19.8)

где х_i – кодирование значение i-го фактора;

Х_i – его фактическое значение;

Х_i,max и Х_i,min – соответственно наибольшее и наименьшее значения i-го фактора в эксперименте (верхний и нижний уровни фактора).

При таком кодировании факторов нижнему уровню соответствует   –1, а верхнему   +1.

Пример12. Повышение производительности прядильных машин, связанное с увеличением частоты вращения веретен и увеличением общей вытяжки, позволяет снизить удельные капитальные вложения и увеличить съем пряжи с 1м² в основном за счет уменьшения количества ровничных и прядильных машин. Однако для того чтобы поддержать на должном уровне качественные показатели пряжи и не получить высокую обрывность, потребуется увеличение трудозатрат. Был проведен специальный эксперимент по изучению влияния повышения производительности кольцепрядильной машины на количество рабочих, необходимое для выработки 1т пряжи. Данные приведены в табл.П15.

Таблица П15 

X1	X2	x1	x2	Y	Y*
10000	30	-1	-1	137,4	137,9
10000	42	-1	0	130,8	138,6
10000	54	-1	+1	137,1	137,7
12000	30	0	-1	127,7	127,7
12000	42	0	0	130,6	130,8
12000	54	0	+1	132,5	132,3
14000	30	+1	-1	151,4	150,9
14000	42	+1	0	155,4	156,4
14000	54	+1	+1	160,7	160,3