1. Система двух дискретных случайных величин.
Рассмотрим систему двух дискретных случайных величин (X,Y) . Пусть X принимает n значений x1, x2…….,xn , а Y принимает k значений y1,y2,…..yk. Закон распределения системы (X,Y) представлен в табл. 1 в шести первых строчках и столбцах. При этом приняты обозначения – pi,j – вероятность совместного появления событий X=xi и Y=yj, т.е., pi,j = P (X=xi & Y=yj). (1.1)
Знак & обозначает «и», т.е. произведение событий.
Таблица 1
|
X/Y |
y1 |
………….. |
yj |
…………. |
yk |
Px |
|
x1 |
p1,1 |
…………. |
p1,j |
…………. |
pk,j |
P |
|
………… |
…………. |
………….. |
………….. |
…………. |
………….. |
………….. |
|
xi |
pi,1 |
…………. |
pi,j |
…………... |
pi,k |
P |
|
………….. |
………….. |
………….. |
………….. |
…………. |
………….. |
………….. |
|
xn |
pn,1 |
………….. |
pn,j |
…………. |
pn,k |
P |
|
Py |
Py1 |
………….. |
Pyi |
…………… |
Pyk |
1 |
Фактически законом распределения системы являются только первые шесть строк и столбцов табл. 1
Пример 1 . В урне 10 шаров. На трех шарах написана дробь 1/2, на двух – 1/3, на четырех – 2/2 и на одном – 2/3. Случайная величина X – значение числителя, Y – значение знаменателя. Тогда закон распределения системы (X,Y) имеет вид
Таблица П1
![]()
|
X/Y |
2 |
3 |
|
1 |
0,3 |
0,2 |
|
2 |
0,4 |
0,1 |
Событие X=xi можно представить в виде суммы попарно несовместимых событий:
(X=xi)=((X=xi & Y=y1) или (X=xi &Y=y2), …., или (X=xi &Y=yk)).
Поэтому
P(X=xi)
=Pxi=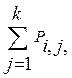 (1.2)
(1.2)
т.е. вероятность события (X=xi) есть сумма вероятностей i-й строки.
Аналогично определяется и вероятность P(Y=yj) = Pyj как сумма вероятностей j-столбца.
Эти вероятности вносятся в седьмые строку и столбец таблицы 1 . Первый и седьмой столбцы определяют закон распределения случайной величины X, взятой отдельно, а первая и седьмая строки – закон распределения случайной величины Y.
Очевидно
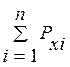 =
=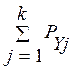 =
= 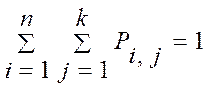 (1.3)
(1.3)
Пример 1 (продолжение). Найдем вероятности Pxi и Pyj.
P(X=1) = 0,3 + 0,2 = 0,5; P(X=2)= 0,4 + 0,1=0,5;
P(Y=2) = 0,3 + 0,4 = 0,7; P(Y=3)=0,2 + 0,1 =0,3
Таблица П1
|
X/Y |
2 |
3 |
Pxi |
|
1 |
0,3 |
0,2 |
0,5 |
|
2 |
0,4 |
0,1 |
0,5 |
|
|
0,7 |
0,3 |
1 |
Из теоремы умножения вероятностей следует, что
Pi,j=P(X=xi & Y=yj) = P(X=xi)P(Y=yj/X=xi)=Pxi Pyj/xi
Отсюда
Pyj/xi=![]() (1.4)
(1.4)
где Pyj/xi – условная вероятность события Y=yj при условии, что X=xi.
Аналогично определяется и условная вероятность P(X=xi/Y=yj) = Pxi/yj.
Условные вероятности определяют условные законы распределения. Обозначим X/yj cлучайную величину X при условии, что Y=yj. Условные распределения приведены в таблице 2 и 3 .
Таблица 2
|
X/yj |
x1 |
L |
xi |
L |
xn |
|
P |
|
L |
|
L |
|
Таблица 3
|
Y/xi |
y1 |
L |
yj |
L |
yk |
|
P |
|
L |
|
L |
|
Условным законам распределения соответствуют условные математические ожидания и условные дисперсии
М(X/yj) = 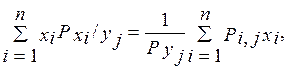 (1.5)
(1.5)
D(X/yj) = ![]()
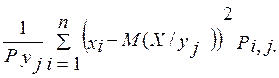 (1.6)
(1.6)
По аналогичным формулам находятся и условные математические ожидания и дисперсии случайной величины Y. Можно использовать для нахождения дисперсии ее свойство.
D (Y/xi) = 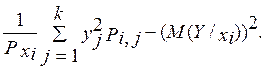 (1.7)
(1.7)
Пример 1 (продолжение). Найдем условные математическое ожидание и дисперсию случайной величины (Y/X=1)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.