M(Y/X=1)=(0,5)-1(2х0,3+3х0,2)=2,4
D(Y/X)= (0,5)-1(2 2х0,2+3 2х0,3) – (2,4)2=0,24 и аналогично
M(Y/X=2)=(0,5)-1(2х0,4+3х0,1)=2,2 и т.д.
Очевидно, что математическое ожидание случайной величины X может быть найдено по формуле
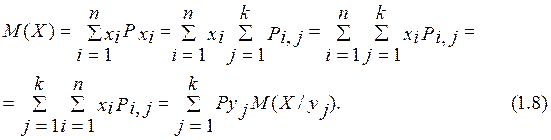
Аналогично определяется и математическое ожидание случайной величины Y.
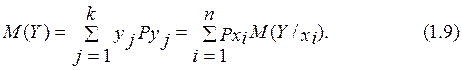
Пример 1 (окончание). Найдем математическое ожидание случайной величины Y
M(Y) = 2*0,7 + 3*0,3 = 2,3 или M(Y) = 0,5*2,4 + 0,5*2,2 = 2,3.
2. Функция распределения системы и ее свойства.
По аналогии с тем, как это было в случае одной случайной величины, закон распределения системы случайных величин (X,Y) может быть задан функцией распределения.
Определение. Функцией распределения системы случайных величин (X,Y) называется такая функция F(x,y), которая определена на всей координатной плоскости xOy равенством
F(x,y) = P(X<x I Y<y). (2.1)
Функции распределения F(x,y) называется также интегральной функцией распределения или интегральным законом распределения
Свойства функции распределения системы аналогичны свойствам функции распределения одной величины.
1.
0![]() F(x,y)
F(x,y) ![]() 1 , так как эта функция равна вероятности.
1 , так как эта функция равна вероятности.
2.
Функция распределения
является неубывающей функцией по каждому из своих аргументов , т.е. если x1<x2 , то F(x1,y)![]() F(x2,y) , и если y1<y2 , то F(x,y1
F(x2,y) , и если y1<y2 , то F(x,y1![]() F(x,y2) , что доказывается так же , как и для функции распределения одной
случайной величины.
F(x,y2) , что доказывается так же , как и для функции распределения одной
случайной величины.
3. События
(X<x &Y<-![]() ), (X<-
), (X<-![]() IY<y), (X<-
IY<y), (X<-![]() IY<-
IY<-![]() )
)
являются невозможными, поэтому
F(x, - ![]() ) = F(-
) = F(- ![]() , y) = F(-
, y) = F(-![]() , -
, -![]() ) = 0.
) = 0.
Здесь и далее используются обозначения lim f(x) = f(![]() .
.
x![]()
4.
Событие (X<x IY<+![]() ) является достоверным, поэтому F(+
) является достоверным, поэтому F(+![]() , +
, +![]() )=1.
)=1.
5.
Событие (X<xIY<+![]() ) – это просто событие (X<x) , поэтому F(x,
+
) – это просто событие (X<x) , поэтому F(x,
+![]() ) = P(X<xIY<+
) = P(X<xIY<+![]() ) = P (X<x) = F1(x) – функция распределения случайной величины
X. Аналогично F (+
) = P (X<x) = F1(x) – функция распределения случайной величины
X. Аналогично F (+![]() , y) = F2 (y) – функции распределения случайной величины
Y.
, y) = F2 (y) – функции распределения случайной величины
Y.
С помощью функции распределения системы можно найти вероятность того, что случайная точка (x,y) попадает в прямоугольную область (см. рис. 1)
![]() Y
Y

![]() d
d
![]()
![]()
![]() c
c
0
a b X
Рис. 1
Введем в рассмотрение три случайных события:
A = (a![]() Тогда сумма этих событий A+B+C =
(Х<b & Y<d). События А и В+С – несовместимы , поэтому
Р(А+В+С)=Р(А) + Р(В+С) = Р(А) + P(B) +Р(С) – Р(ВС) , но событие ВС=(Х<a &
Y<c). Таким образом мы получаем
Тогда сумма этих событий A+B+C =
(Х<b & Y<d). События А и В+С – несовместимы , поэтому
Р(А+В+С)=Р(А) + Р(В+С) = Р(А) + P(B) +Р(С) – Р(ВС) , но событие ВС=(Х<a &
Y<c). Таким образом мы получаем
Р(Х<b.&.Y<d)=P(a![]() X<b.&.c
X<b.&.c![]() Y<d)+P(X<a.&.Y<d)+P(X<b,&,Y<c)-P(X<a.&.Y<c)
Y<d)+P(X<a.&.Y<d)+P(X<b,&,Y<c)-P(X<a.&.Y<c)
или
F(b,d)
= P(a![]() X<b.&.c
X<b.&.c![]() Y<d)+F(a,d)+F(b,c)-F(a,c).
Y<d)+F(a,d)+F(b,c)-F(a,c).
Отсюда следует, что
Р(a![]() X<b.&.c
X<b.&.c![]() Y<d)=F(b,d)-F(a,d)+F(a,c).
(2.2)
Y<d)=F(b,d)-F(a,d)+F(a,c).
(2.2)
Отметим в заключение, что все перечисленные свойства и формулы не зависят от того, являются ли случайные величины, входящие в систему, дискретными или нет. В случае, если компоненты системы – дискретные случайные величины, то F(x,y) – ступенчатая функция.
3. Системы двух случайных величин. Плотность системы.
Определение системы непрерывных случайных величин и плотность системы вводятся аналогично тому, как это было введено для одной случайной величины.
Определение 1. Система
случайных величин (X,Y) называется непрерывной, если множество
возможных значений (x,y) занимает сплошь некоторую область ![]() плоскости xOy ( в данном случае всю
координатную плоскость), функция распределения системы F(x,y) непрерывна на
всей плоскости xOy и имеет внутри области
плоскости xOy ( в данном случае всю
координатную плоскость), функция распределения системы F(x,y) непрерывна на
всей плоскости xOy и имеет внутри области ![]() непрерывную
смешанную производную второго порядка.
непрерывную
смешанную производную второго порядка.
Определение 2. Плотностью вероятности системы (X,Y) в точке (x,y)![]() называется предел отношения
вероятности попасть в некоторую область D
называется предел отношения
вероятности попасть в некоторую область D![]()
![]() , содержащую эту точку, к площади D при
условии, что область D стягивается в эту точку.
, содержащую эту точку, к площади D при
условии, что область D стягивается в эту точку.
Плотность вероятности системы или просто плотность обозначается f(x,y) и называется также дифференциальной функцией распределения или дифференциальным законом распределения системы.
Возьмем производственную точку (x,y)![]() и
рассмотрим прямоугольник с вершиной в этой точке и сторонами
и
рассмотрим прямоугольник с вершиной в этой точке и сторонами ![]() и
и ![]() .
На основании определения 2 можно написать
.
На основании определения 2 можно написать
f(x,y) = lim ![]()
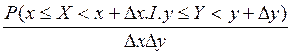 .
.
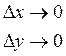
Используя формулу (2.2) и правило последовательного перехода к пределу , получим
f(x,y)
= lim 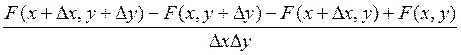 =
=
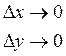
= lim 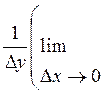
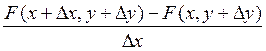 -
- 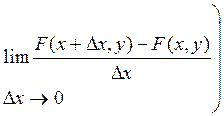 =
=
= lim 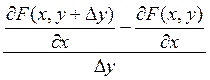 =
= 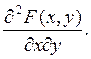
y![]()
Рассмотрим двойной интеграл от плотности по прямоугольнику представленному на рисунке 1.
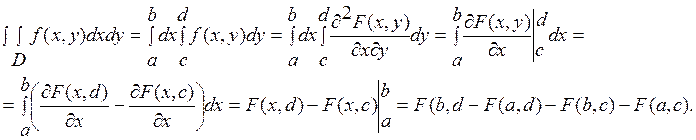
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.