Моменты системы случайных величин. Коэффициент корреляции. Условия независимости случайных величин

Таблица 4

Таблица  5

Табл. 4 и 5 представляют собой  функциональные зависимости математического ожидания одной величины от значения другой. Из формул (4.7) и (4.8) следует, что

М(Y/x) =                      (4.9)       

M(X/y) = ,                    (4.10)

т.е.  они тоже определяют математическое ожидание одной величины от значения другой называются уравнениями регрессии, а их графики – линиями регрессии.(Уравнения регрессии 1-го рода)

Табл. 4 и формула (4.9) – уравнение регрессии Y на x, а табл. 5 и формула (4.10) – уравнение регрессии X и на y, а на оси ординат Y и M (Y/x) (обе линии регрессии строятся на одном графике).

Пример 2 (продолжение). Найдем условные плотности X и Y системы, распределенной равномерно в круге, т.е. системы с плотностями

f(x,y)=   f₁(x) = 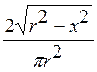        f₂(y) = .

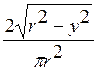По формулам (4.5) и (4.6) находим условные плотности.

f₁(x/y) = , f₂(y/x)=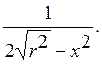

Используя формулы (4.7) и (4.8) , находим условные математические ожидания

M(Y/x) =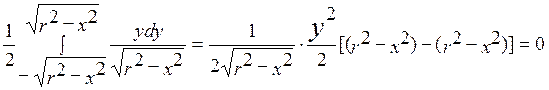   

M(X/y)=0

и условные дисперсии

D(Y/x) =

В этом примере линии регрессии – прямые, совпадающие с осями координат.

2.  Моменты системы случайных величин. Коэффициент корреляции.

Как и в случае одной случайной величины, для системы двух случайных величин вводятся моменты.

Определение 1 .   Центральным моментом s- го, r-го порядков системы случайных величин (X,Y) называется математическое ожидание произведения s-й степени отклонения одной величины на r-ю степень отклонения другой от своих математических ожиданий.

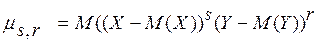                 (5.1)

Для дискретных величин момент s-го , r-го порядка находится по формуле

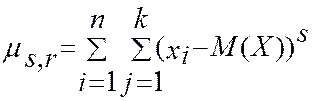(y_j-M(Y))P_{i,j ,}

а для непрерывных –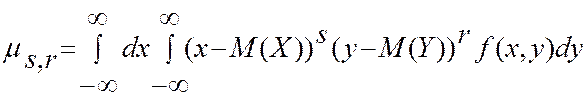                   

.

Очевидно,

Определение 2.  Центральный момент первого порядка называется корреляционным моментом.

          (5.2)

Корреляционный момент обладает следующим свойством: корреляционный момент равен математическому ожиданию произведения случайных величин без произведения их математических ожиданий, т.е.

                              (5.3)

Для удобства дальнейшего изложения будем использовать обозначения:

М(X) = m_x,  M(Y) = m_y,  D(X) =  и  Тогда

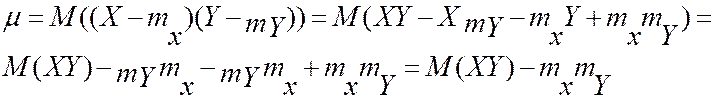
Размерность корреляционного момента равна произведению размерностей случайных величин, поэтому вводится безразмерная величина – коэффициент корреляции.

Определение 3.  Коэффициентом корреляции называется отношение корреляционного момента к произведению средних квадратических отклонений.

Коэффициент корреляции обозначается обычно r, или r (X,Y), или r_x,y и по определению

r=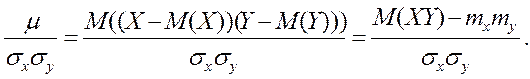                     (5.4)

1-е свойство коэффициента корреляции.

Значение коэффициента корреляции ограничено -1 .

Рассмотрим случайную величину Z(t), где t –неслучайный параметр

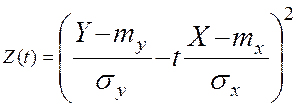
Очевидно, при любом значении t  Z(t), а следовательно, и математическое ожидание (среднее значение) этой величины тоже неотрицательно, т.е. M(Z(t)) , при любом t. Но

= .

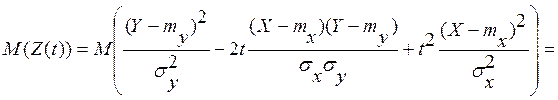
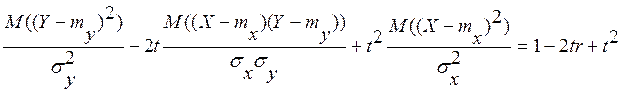Таким образом, квадратный трехчлен t²-2tr+1 при любом значении аргумента t, а следовательно, дискриминант этого трехчлена неположителен, т.е. 4r²-4, или r1, следовательно, |r|1 , или -1 , что и требовалось доказать.

3.  Условия независимости случайных величин.

Напомним определение независимости двух случайных величин. Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какое значение приняла другая.

Теорема 1 (необходимое условие независимости или 2-е свойство коэффициента корреляции).

Если случайные величины независимы, то коэффициент корреляции равен нулю.