Моменты системы случайных величин. Коэффициент корреляции. Условия независимости случайных величин, страница 2

Действительно для независимых случайных величин математическое ожидание произведения равно произведению математических ожиданий, т.е. M(XY) = m_xm_y, поэтому  и, следовательно, r=0, что и требовалось доказать.

Замечание. Обратное утверждение, вообще говоря, неверно. Рассмотрим случайную величину X , подчиненную нормальному закону распределения с математическим ожиданием а=0 и дисперсией ² = 1. Как мы знаем, для нормального закона коэффициент асимметрии равен нулю, т.е.

As = 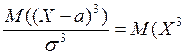)=0.

Рассмотрим случайную величину Y=X² и найдем коэффициент корреляции

R(X,Y) = 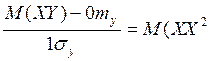)=M(X³)=0.

В этом примере случайные величины зависимы (они связаны функциональной зависимостью), и несмотря на это, коэффициент корреляции равен нулю.

Определение. Случайные величины, коэффициент корреляции которых равен нулю, называется некоррелированными и являются подозрительными на независимость.

Пример 3. Рассмотрим систему случайных величин (X,Y), закон распределения которой приведен в таблице П3

Таблица П3

Y	- 1	0	1	Px
X
1	0,24	0,30	0,06	0,6
2	0,16	0,20	0,04	0,4
Py	0,4	0,5	0,1	1

Найдем числовые характеристики этой величины.

m_x=1х0,6+2х0,4=1,4      M(X²)=1х0,6+4х0,4=2,2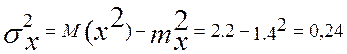  

m_y=-1х0,4+1х0,1=-0,3   M(Y²)=1х0,4+1х0,1=0,5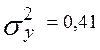     

M(XY) = -1х1х0,24-1х2х0,16+1х1х0,06+1х2х0,04=-0,42 и

r= 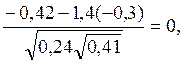 таким образом случайные величины X и Y некоррелированы, т.е. подозрительны на независимость.

Теорема 2( условие независимости дискретных случайных величин). Для того чтобы случайные величины были независимы, необходимо и достаточно, чтобы

Для всех I и j см. табл. 1

Составим закон распределения случайной величины X , для чего выберем из табл. 1 первый столбцы (см. табл. 6)

Таблица 6

X	x1	……..	xi	……...	xn
Px	P	……..	P	……...	P

и рассмотрим табл. 2, приведенную в пас. 5

Таблица 2

X/yi	x1	L	xi	L	xn
P		L		L

Необходимость. Дано: X и Y – независимы. Тогда табл. 2 не зависит от значения Y, т.е. совпадает с таблицей 6. Следовательно, 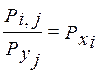  или   , что и требовалось доказать.

Достаточность. Дано: 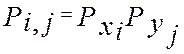. Тогда  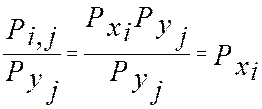  и табл. 2 совпадает с таблицей 6  , т.е. закон распределения X и Y независимы. Действительно: 0,4х0,6=0,24;   0,4х0,4=0,16;   0,5х0,6=0,30;    0,5х0,6=0,30;  0,5х0,4=0,20;   0,1х0,6=0,06;

0,1х0,4=0,04 , т.е. выполнено условие независимости и X и Y независимы.

Теорема 3 (Условие независимости непрерывных случайных величин). Для того чтобы случайные величины были независимы необходимо и достаточно, чтобы плотность системы равнялась произведению плотностей величин, составляющих эту систему.

Необходимость. Дано: X и Y – независимы, т.е. закон распределения одной из них, скажем X, не зависит от значения Y, но закон распределения определяется плотностью, следовательно, плотность X не зависит от значения Y

-f₁(x/y)=f₁(x) , но тогда в соответствии с формулой (4.6)

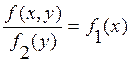или f (x,y)=f₁(x)f₂(y).

Достаточность.  Дано   f (x,y)=f₁(x)f₂(y).  В соответствии с формулой (4.6)

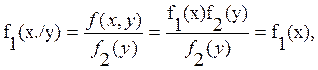 т.е.  закон распределения X, определяемый плотностью, не зависит от значения величины Y, следовательно, X и Y  независимы.

Упражнение1.  Доказать, что составляющие системы случайных величин, распределенных равномерно в круге (см. пример 2) некоррелированы, но зависимы.