Необходимость. Дано: X и Y – независимы, т.е. закон распределения одной из них, скажем X, не зависит от значения Y, но закон распределения определяется плотностью, следовательно, плотность X не зависит от значения Y
-f1(x/y)=f1(x) , но тогда в соответствии с формулой (4.6)
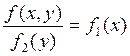 или f
(x,y)=f1(x)f2(y).
или f
(x,y)=f1(x)f2(y).
Достаточность. Дано f (x,y)=f1(x)f2(y). В соответствии с формулой (4.6)
f1(x/y)= 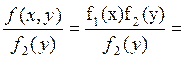 f1(x),
т.е. закон распределения X, определяемый плотностью, не зависит от значения
величины Y, следовательно, X и Y независимы.
f1(x),
т.е. закон распределения X, определяемый плотностью, не зависит от значения
величины Y, следовательно, X и Y независимы.
Упражнение1. Доказать, что составляющие системы случайных величин, распределенных равномерно в круге (см. пример 2) некоррелированы, но зависимы.
2. Двухмерный нормальный закон распределения.
Система случайных величин (X,Y) подчиняется двухмерному нормальному закону распределения , если она определена на всей координатной плоскости xOy и плотность системы определяется формулой
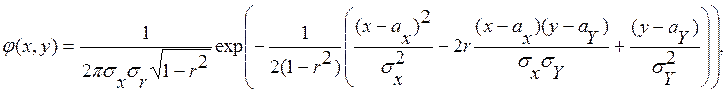 (7.1)
(7.1)
где aX , aY - математические ожидания случайных величин X, Y;
![]() - дисперсии этих
величин;
- дисперсии этих
величин;
r – их коэффициент корреляции, причем -1<r<1.
Отметим, что здесь, как и в случае одной случайной
величины, плотность нормального закона обозначается не буквой f, а буквой ![]() .
.
3-е свойство коэффициента корреляции или условие независимости нормальных случайных величин. Если случайные величины X и Y подчиняются нормальному закону и коэффициент корреляции равен нулю, то случайные величины независимы.
Действительно, пусть r=0 , тогда плотность (7.1) будет иметь вид
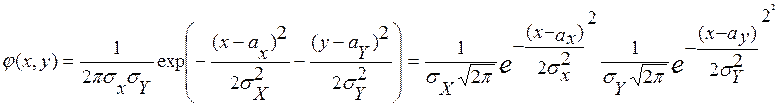 =
= ![]() где
где ![]() и
и
![]() – плотности величин X и Y
соответственно.
– плотности величин X и Y
соответственно.
Таким образом, выполняется условие независимости непрерывных случайных величин и, следовательно, X и Y независимы. Как мы видим, для случайных величин, имеющих нормальный закон распределения, необходимое условие независимости становится достаточным.
3. Условные плотности системы нормальных случайных величин.
Прямые регрессии.
Для удобства преобразований введем обозначения
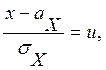 (8.1)
(8.1)
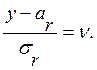 (8.2)
(8.2)
Тогда плотность системы (7.1) можно записать так
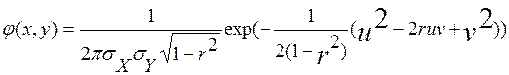 ,
,
а плотность нормальной случайной величины X
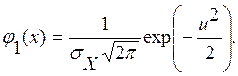
Условная плотность(4.5) будет равна
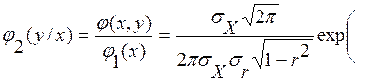
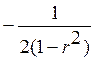 (u2-2ru
(u2-2ru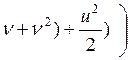
Отметим, что функция y=exp(x) – это показательная функция y=ex, поэтому при делении аргумента этой функции (показатели степени) вычитаются. Преобразуем отдельно показатель степени
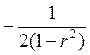 (u2-2ru
(u2-2ru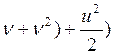 =
= 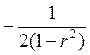
(u2-2ru![]()
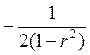 (
(![]()
Учитывая формулы (87.1) и (8.2) , получим , что показатель степени равен
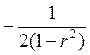
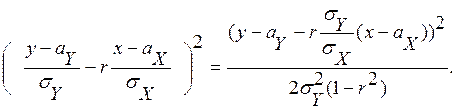
Таким образом, условная плотность равна
![]() =
= 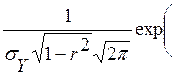 -
-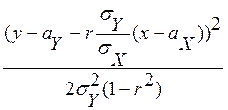
![]() . (8.3)
. (8.3)
Это плотность нормальной случайной величины
![]() =
= 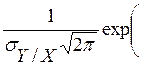 -
-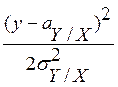
![]() ,
,
где ay/x
– условное
математическое ожидание, а ![]() - условная
дисперсия случайной величины Y при условии, что X=x. Поэтому уравнение
регрессии (4.9) для случайных величин, подчиненных нормальному закону, имеет
вид
- условная
дисперсия случайной величины Y при условии, что X=x. Поэтому уравнение
регрессии (4.9) для случайных величин, подчиненных нормальному закону, имеет
вид
M(Y/x)
= aY + r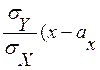 ). (8.4)
). (8.4)
Аналогично, в силу симметричности плотности ![]() получим и уравнение регрессии X и Y
получим и уравнение регрессии X и Y
M(X/y)
= ax + r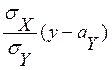 . (8.5)
. (8.5)
Условные дисперсии соответственно равны
D(Y/x)=![]() ) ,
) ,
D (X/y)=![]() ).
).
Функции (8.4) и (8.5) – линейные , следовательно , линии регрессии – прямые , причем обе они проходят через центр распределения системы , т.е. через точку с координатами ( ax,aY)
Известная формула нахождения «нормального веса» человека по его росту V=L-100, где V – вес, кг; а L – рост, см, есть не что иное, как уравнение регрессии и V – это средний вес для роста L.
Условные коэффициенты прямых регрессии равны
kx/Y=r![]() kY/x=r
kY/x=r![]() (8.6)
(8.6)
и знаки угловых коэффициентов совпадают со знаком коэффициента корреляции, поэтому, если r>0, то прямые регрессии (8.4) и (8.5) обе возрастающие, а если r<0, то обе прямые – убывающие. Это позволяет сформулировать еще два свойства коэффициента корреляции:
4-е свойство коэффициента корреляции. Если система случайных величин подчиняется нормальному закону и коэффициент корреляции удовлетворяет неравенству -1<r<0, то с возрастанием значения одной величины другая в среднем убывает.
4-е свойство коэффициента корреляции. Если система случайных величин подчиняется нормальному закону и коэффициент корреляции удовлетворяет неравенству 0<r<1, то с возрастанием значения одной величины другая в среднем тоже возрастает.
На рис. 2 приведены условные плотности X для некоторых значений Y и прямая регрессии для r>0.
9. Средняя квадратическая регрессия.
Рассмотрим систему случайных величин (X,Y). Подберем такую функцию f(x), чтобы средний квадрат отклонения случайной величины Y от этой функции случайной величины X был минимальным, т.е. чтобы эта функция обеспечивала минимум математического ожидания квадрата отклонения Y от f(X). Иными словами, стоит задача из всех возможных функций выбрать такую, которая обеспечивает
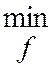
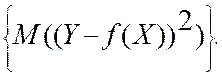
![]() (9.1)
(9.1)
Доказано, что этот минимум достигается, если f(x)
![]() , определяемой уравнением регрессии Y на X
(4.9). Однако, если уравнение регрессии неизвестно, то найти такую функцию из
(9.1) невозможно. Поэтому решают задачу отыскания минимума выражения (9.1) для
функций данного вида f(A,x), где A= (a1,….a
, определяемой уравнением регрессии Y на X
(4.9). Однако, если уравнение регрессии неизвестно, то найти такую функцию из
(9.1) невозможно. Поэтому решают задачу отыскания минимума выражения (9.1) для
функций данного вида f(A,x), где A= (a1,….a![]() ) – вектор коэффициента этой функции, т.е. ищется не
сама функция обеспечивающая минимум среднего квадрата отклонения Y от f(X)
, а определяются коэффициенты заранее выбранной функции (например, линейной
определяются коэффициенты заранее выбранной функции (например, линейной y=x+b,
или квадратичной y=ax2+bx+c, или функции какого-нибудь другого вида) так,
чтобы из всех функций выбранного вида, функция с этими коэффициентами
обеспечивала минимум среднего квадрата отклонения Y
от f(A,X). Иными словами, нужно найти такой вектор
коэффициента А, чтобы функция
) – вектор коэффициента этой функции, т.е. ищется не
сама функция обеспечивающая минимум среднего квадрата отклонения Y от f(X)
, а определяются коэффициенты заранее выбранной функции (например, линейной
определяются коэффициенты заранее выбранной функции (например, линейной y=x+b,
или квадратичной y=ax2+bx+c, или функции какого-нибудь другого вида) так,
чтобы из всех функций выбранного вида, функция с этими коэффициентами
обеспечивала минимум среднего квадрата отклонения Y
от f(A,X). Иными словами, нужно найти такой вектор
коэффициента А, чтобы функция ![]()
![]() переменных
переменных
S=(A)=S(![]() ) = M((Y-f(A,X))2)
(9.2)
) = M((Y-f(A,X))2)
(9.2)
достигала минимума.
Пусть A*=(a![]() ,……, a
,……, a![]() ) обеспечивает этот минимум, т.е. является точкой
минимума функции S(A). Тогда уравнение y=f(A*, x)
называется уравнением средней квадратической регрессии, а случайная
величина Y* = f(A*, X) приближением случайной величины Y функций данного
вида случайной величины X ,найденной по методу наименьших квадратов (МНК).
Коэффициенты этой функции А*=(a
) обеспечивает этот минимум, т.е. является точкой
минимума функции S(A). Тогда уравнение y=f(A*, x)
называется уравнением средней квадратической регрессии, а случайная
величина Y* = f(A*, X) приближением случайной величины Y функций данного
вида случайной величины X ,найденной по методу наименьших квадратов (МНК).
Коэффициенты этой функции А*=(a![]() ,……, a
,……, a![]() ) называется коэффициентами регрессии.
) называется коэффициентами регрессии.
10. Линейное уравнение средней квадратической регрессии.
Рассмотрим систему случайных величин (X,Y) , имеющих
математические ожидания mx и mY , дисперсии ![]() и
и ![]() и коэффициент корреляции r
. Найдем линейное уравнение средней квадратической регрессии, т.е. коэффициенты
линейной функции y=kx+b. Для этого найдем минимум функции
и коэффициент корреляции r
. Найдем линейное уравнение средней квадратической регрессии, т.е. коэффициенты
линейной функции y=kx+b. Для этого найдем минимум функции
S(k,b)=M((Y-kX-b)2). (10.1)
Возведем в квадрат выражение под знаком математического ожидания и воспользуемся свойствами математического ожидания
S(k,b)=M(Y2+k2X2 +b2 – 2 kXY-2bY+2kbX) = M(Y2)+k2M(X2)+b2-2kM(XY)-2bM(Y)+2kbM(X)
Учитывая формулы
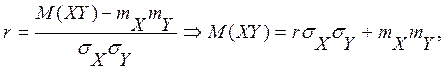
![]()
![]() ,
,
получим
![]() +k2(
+k2(![]() )+b2-2k(r
)+b2-2k(r![]() )-2 b
)-2 b![]() Y+2kbmX.
Y+2kbmX.
Чтобы найти минимум этой функции, нужно найти точки, подозрительные на экстремум, а для этого найти частные производные и приравнять их к нулю.
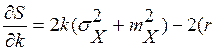
![]() )+2bmx
)+2bmx
![]() =2b-2mY+2kmX
=2b-2mY+2kmX
Приравняем частные производные к нулю, при этом сократим все члены на 2 и перенесем известные в правую часть. Получим систему
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.