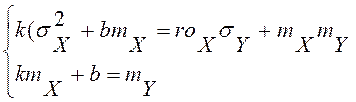Остаток случайной величины. Свойство коэффициентов корреляции. Система n случайных величин

                                                                  (10.2)

Решив эту систему , получим

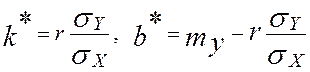                                                                     (10.3)

Тогда линейное уравнение средней квадратической регрессии будет иметь вид

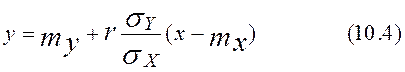                                                а приближение случайной величины Y в виде линейной функции X по методу наименьших квадратов

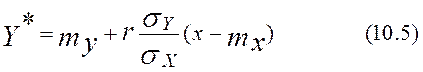
(Отметим, что уравнение средней квадратической регрессии (10.4) совпадает с уравнением регрессии Y на X для нормального закона (7.9), что естественно должно быть в силу сказанного выше о решении задачи минимизации (9.1)).

Из (10.5) следует еще два свойства коэффициента корреляции.

6-е свойство коэффициента корреляции. Если -1<r<0, то с возрастанием значения одной величины, другая – имеет тенденцию к убыванию.

Действительно, если -1<r<0, то с возрастанием величины X в силу (10.5) Y* убывает. Но Y* является линейным приближением случайной величины  Y, следовательно эта величина имеет тенденцию к убыванию.

7-е свойство коэффициента корреляции. Если 0<r<1, то с возрастанием значения одной величины, другая – имеет тенденцию к возрастанию.

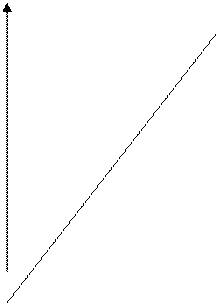
Действительно в этом случае Y* возрастает с увеличением значения X в силу (10.5), и Y, приближением которого является Y*, имеет тенденцию к возрастанию. Это не означает, что если имеется  два значения системы (X,Y) (x₁,y₁) и (x₂,y₂), то при x₁>x₂ обязательно y₁>y₂ , но более вероятно, что при x₁>x₂ мы будем наблюдать y₁>y₂, чем наоборот. Если же провести достаточно большое число испытаний этой системы, то точки (x,y) в основном расположатся вблизи прямой (10.5) , как это показано на рис. 3, т.е. с достаточно высокой вероятностью случайные точки попадут в выделенную область, чем за ее пределы, даже если область возможных значений системы – вся координатная плоскость.

Y

                               Y^*                                            

X

                              Рис. 3.

11.  Остаток случайной величины.      

Пусть система случайных величин (X,Y) имеет числовые характеристики m_X, m_Y, 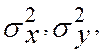 и r. Y^* - линейное приближение Y как функции X (10.5). Тогда случайная величина

Z=Y-Y^*                                            (11.1)

Называется остатком случайной величины Y после исключения линейного (главного) влияния на нее случайной величины X  или просто остатком величины Y. Вариация остатка может быть обусловлена как нелинейным влиянием X, так и влиянием других случайных величин, несвязанных с X.

Исследуем остаток

Z=Y-Y^*  = Y-m_Y-r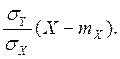         (11.2)

Найдем числовые характеристики, т.е. его математическое ожидание и дисперсию остатка.

M(Z) =M(Y- m_Y)- r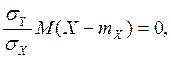                

D(Z) =M(Z²) = M ((Y-m_Y)²-2r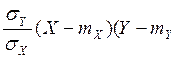 ) + r²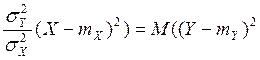) =D(Y) – 2r).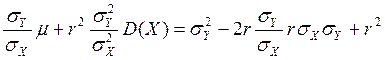

Пусть |r| = 1 . Тогда D=(Z) =0 , таким образом Z не имеет вариации, т.е. является величиной постоянной. Но M(Z) =0 и, следовательно, Z=0 или Y = Y^* , т.е. Y есть линейная функция X. Отсюда следует еще два свойства коэффициента корреляции.

8-е свойство коэффициента корреляции. Если r=-1, то Y есть линейная убывающая функция X

Y = m_r -).

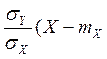9-е свойство коэффициента корреляции. Если r=1, то Y есть линейная возрастающая функция X              

Y = m_r +).

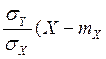Рассмотрим дисперсию остатка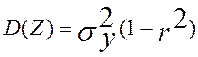 и найдем из этого равенства r²

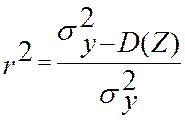
Числитель этой дроби можно рассматривать как характеристику линейного влияния X и Y. Действительно, из дисперсии Y вычитается дисперсия как бы всего кроме линейного влияния, т.е. остается часть дисперсии связанная с линейным влиянием X, а в знаменателе полная дисперсия Y. Поэтому квадрат коэффициента корреляции показывает, какая  доля общей вариации Y вызвана линейным влиянием X. Обычно определяют не долю, а процент вариации Y.