Остаток случайной величины. Свойство коэффициентов корреляции. Система n случайных величин, страница 2

Определение. Величина d= 100r² называется коэффициентом детерминации. Коэффициент детерминации показывает, какой процент вариации одной величины вызван линейным влиянием другой.

Отметим, что мы все время говорили о влиянии случайной величины X на случайную величину Y. В силу равноправности случайных величин, входящих в систему, можно говорить о влиянии Y на X . Поэтому уже в определении коэффициента детерминации говорится о влиянии одной величины на другую. Из всего выше сказанного следует, что коэффициент корреляции является характеристикой тесноты линейной связи между величинами.

Пример 4. Рассмотрим систему двух дискретных случайных величин и исследуем наличие, характер и тесноту линейной связи между ними.

Таблица П4

X/Y	-1	0	1	px
1	0	0	0,3	0,3
2	0,1	0,3	0,1	0,5
3	0,2	0	0	0,2
pY	0,3	0,3	0,4	1

Найдем числовые характеристики этой системы

M_X = 0,3 + 1 + 0,6 =1,9; m_Y= - 0,3 + 0,4 = 0,1 ;

M(X²)=0,3 + 2 + 1,8 = 4,1 ;  M(Y²)=0,3 + 0,4 = 0,7 ;

(X) = 4,1 – 1,9= 0,49; (Y) = 0,7 – 0,1= 0,69 ;

M(XY) = 0,3 – 0,2 + 0,2 – 0,6 = - 0,3 ;

 

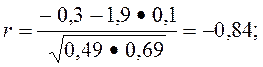
Таким образом, случайные величины X и Y коррелированны, т.е. между ними существует линейная связь. С возрастанием значения одной величины другая имеет тенденцию к убыванию. 70,6% вариации одной величины вызвано линейным влиянием другой.

12. Свойство коэффициентов корреляции

Коэффициент корреляции является характеристикой тесноты линейной связи между двумя случайными величинами.

1.  Коэффициент корреляции r по модулю не превышает единицы, т.е.

2.  Если  то величины связаны линейной функциональной зависимостью, одна величина является линейной убывающей функцией другой.

3.   Если  то с возрастанием значения одной величины, другая – имеет тенденцию к убыванию.

4.  Если  и случайные величины распределены по нормальному закону, то с возрастанием значения одной величины, другая – убывает в среднем,т.е. убывает её математическое ожидание.

5.  Если  то величины некоррелированы, между ними отсутствует линейная связь и они подозрительны на независимость.

6.  Если  и случайные величины распределены нормальному закону, то они независимы.

7.  Если  то с возрастанием значения одной величины другая имеет тенденцию к возрастанию.

8.  ?????????????????Если  и случайные величины распределены по нормальному закону, то с возрастанием значения одной величины, другая – возрастает в среднем.

9.  Если  то величины связаны линейной функциональной зависимостью, одна величина является линейной возрастающей функцией другой.

10.  Величина  называется коэффициентом детерминации и показывает, какой процент вариации (дисперсии) одной величины вызван линейным влиянием другой.

Замечание. Завершая рассуждения о зависимости случайных величин, отметим, что между независимостью и самой тесной, т.е. функциональной зависимостью имеются промежуточные формы зависимости, когда каждому значению одной величины, соответствует свой закон распределения другой. В частном случае, если исследуется линейная зависимость, то её называют корреляционной. Как охарактеризовать тесноту нелинейной связи между величинами, мы рассмотрим ниже.

13. Система n случайных величин

Рассмотрим систему n случайных величин

(X₁,X₂,..,X_n)                               (13.1)

Она характеризуется неслучайным вектором математических ожиданий

(m₁,m₂,..,m_n)                               (13.2)

неслучайным вектором дисперсий

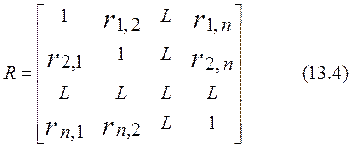
где Очевидно, что матрица (13.4) является симметричной, так как