В приводе винта судна на подводных крыльях, как показывает рис. 7, б, в диапазоне скоростей, соответствующем выходу на крыло, неизбежно возникают неустойчивые режимы. Такие двигатели также снабжаются всережимными регуляторами скорости.
в) Транспортный дизель
Совмещенные характеристики подвода и отвода транспортного дизеля показаны на рис. 8. Малая крутизна нарастания характеристик нагрузки с увеличением скорости в сочетании с тенденцией к росту крутящего момента на малых нагрузках приводит к тому, что режимы работы транспортной двигательной установки устойчивы только на больших и средних нагрузках.
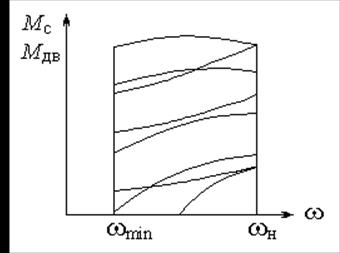
 Сброс нагрузки даже на устойчивых
режимах приводит к недопустимому повышению частоты вращения. Поэтому транспортный дизель
должен быть как минимум защищен от превышения допустимой скорости.
Неустойчивость режимов малых нагрузок и холостого хода приводит к невозможности
оставить без управления двигатель, работающий на минимальных оборотах холостого
хода (остановочные и стояночные режимы) – при этом в равной мере возможен
разнос или самопроизвольная остановка двигателя. Поэтому для таких двигателей
обязательным является также автоматическое поддержание минимальной частоты
вращения.
Сброс нагрузки даже на устойчивых
режимах приводит к недопустимому повышению частоты вращения. Поэтому транспортный дизель
должен быть как минимум защищен от превышения допустимой скорости.
Неустойчивость режимов малых нагрузок и холостого хода приводит к невозможности
оставить без управления двигатель, работающий на минимальных оборотах холостого
хода (остановочные и стояночные режимы) – при этом в равной мере возможен
разнос или самопроизвольная остановка двигателя. Поэтому для таких двигателей
обязательным является также автоматическое поддержание минимальной частоты
вращения.
Вопрос о необходимости автоматического
поддержания заданной частоты вращения на промежуточных, достаточно устойчивых
режимах должен решаться с учетом конкретных особенностей транспортного
средства. Наличие такого регулирования облегчает работу водителя, позволяя
поддерживать постоянную скорость движения при изменениях нагрузки (подъемы,
спуски).
С другой стороны, высокая чувствительность регулятора к отклонениям скорости
приводит к значительным изменениям подачи при небольших колебаниях нагрузки,
что отрицательно сказывается на экономичности работы двигателя. Поэтому,
например, в тракторных установках, где постоянство скорости движения часто
диктуется технологическими требованиями, а водитель должен следить за
прицепными и навесными орудиями, необходимо поддержание заданной скорости на
всех режимах (всережимный регулятор). Автомобильный двигатель может иметь как
всережимный, так и двухрежимный регулятор. В последнем случае подача топлива
управляется регулятором только на максимальной и минимальной скорости, а на
промежуточных режимах – непосредственно водителем.
г) Генераторные установки
Привод генератора переменного тока должен обеспечивать постоянство частоты вращения с минимальными отклонениями в целях поддержания напряжения и частоты тока в сети. Несмотря на достаточную устойчивость основных режимов работы мото- и дизель-генераторов, сочетание характеристик подвода и отвода не обеспечивает выполнение этого требования. Поэтому двигатель, предназначенный для работы с генератором, должен быть снабжен однорежимным прецизионным регулятором, поддерживающим одно заданное значение частоты вращения с высокой точностью.

 Для вывода дифференциального
уравнения двигателя как объекта САРС воспользуемся методом малых отклонений.
Момент двигателя является функцией частоты вращения w и параметра х, определяющего
подачу топлива (положения рейки топливного насоса или дроссельной заслонки).
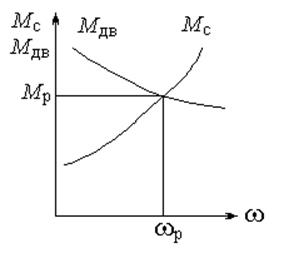
Момент сопротивления зависит от частоты вращения и параметра нагрузки L (рис. 9):
Для вывода дифференциального
уравнения двигателя как объекта САРС воспользуемся методом малых отклонений.
Момент двигателя является функцией частоты вращения w и параметра х, определяющего
подачу топлива (положения рейки топливного насоса или дроссельной заслонки).
Момент сопротивления зависит от частоты вращения и параметра нагрузки L (рис. 9):
Мдв = Мдв(w,х) ; Мс = Мс(w,L) .
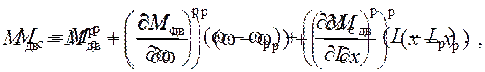
В соответствии с принципом
малых отклонений, рассматриваем эти функции вблизи точки равновесия. Тогда при
разложении в ряд можно оставить только первые производные:
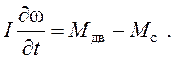
Дифференциальное уравнение вала
двигателя с присоединенными массами приводного агрегата с суммарным моментом
инерции I:
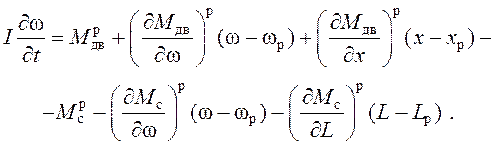 |
|||
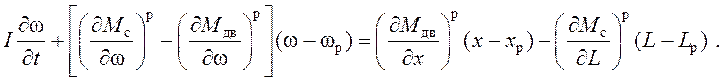 |
|||
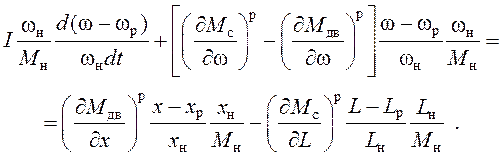 |
|||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.