у1 = х (ДА, логическое повторение), или
![]() (НЕ, логическое отрицание).
(НЕ, логическое отрицание).
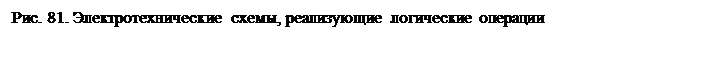 Электротехнические
схемы, реализующие эти логические операции, показаны на рис. 81, а.
Электротехнические
схемы, реализующие эти логические операции, показаны на рис. 81, а.
Логическая ячейка, имеющая два входных параметра и один выходной, выполняет одну из следующих операций:
у1 = х1 + х2 (ИЛИ, логическое сложение);
у2 = х1 ´ х2(И, логическое умножение);
у3 = х1~ х2(равнозначность);
у4 = х1Å х2 (неравнозначность);
у5 = х1¯ х2 (ИЛИ-НЕ);
у6 = х1 / х2(И-НЕ).
Ниже приведена таблица значений у в зависимости от комбинаций х1 и х2.
|
х1 |
х2 |
у1 |
у2 |
у3 |
у4 |
у5 |
у6 |
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
Электротехнические схемы, реализующие функции ИЛИ и И, показаны на рис. 81, б, в. Остальные функции могут быть заменены комбинацией операций И, ИЛИ и НЕ.
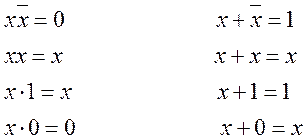
Основные тождества алгебры Буля
Переместительный закон
х1 х2 = х2 х1
х1 + х2 = х2+ х1
Сочетательный закон
х1 (х2 х3) = (х1 х2) х3 = х2 (х1 х3)
х1 + (х2 + х3) = (х1 + х3) + х2
Распределительный закон
(х1 х2) + х3 = (х1 + х3)(х2 + х3)
(х1 + х2) х3 = х1 х3 + х2 х3
УЛУ комбинационного типа строится в следующем порядке:
1. Составляется алгоритм функционирования системы.
2. Входные параметры обозначаются символом х, выходные у и на основании алгоритма строится таблица состояний. Пример такой таблицы для системы, имеющей три входных параметра и два выходных, показан ниже (параметры системы выбраны произвольно):
|
х1 |
х2 |
х3 |
у1 |
у2 |
|
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
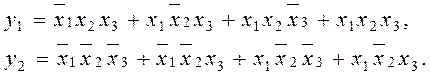 |
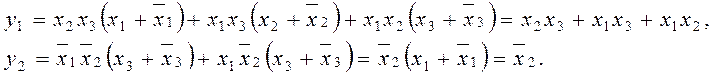 |
5. На основе логических выражений строятся блок-схемы. На рис. 82, а показана схема, соответствующая исходному виду выражения для у1. Как видно, схема получается весьма громоздкой, в отличие от схемы на рис. 82, б, построенной по упрощенным выражениям.
6. Подбираются функциональные элементы, реализующие требуемые логические операции, и строится электрическая схема. Следует заметить, что даже при использовании микропроцессорных программируемых схем про-граммирование осуществляется в терминах логических ячеек и выражений.
В управляющих устройствах
последовательностного типа выходные сигналы зависят не только от комбинации
входных сигналов, но и от последовательности их поступления. Из этого вытекает
необходимость 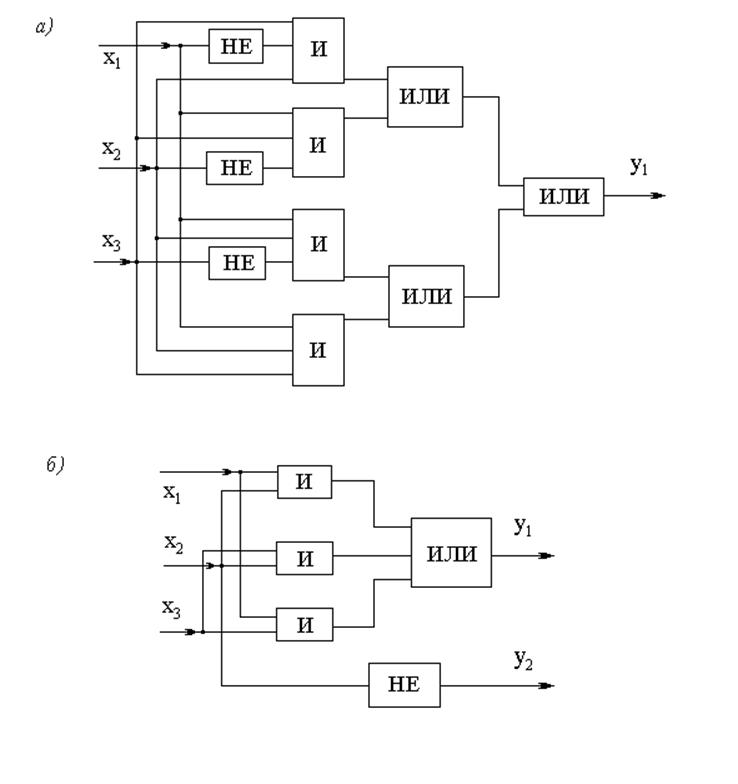
включения в такие УЛУ элементов
типа "память", фиксирующих текущее состояние системы. Таким образом,
УЛУ такого типа включает комбинационную часть К (рис. 83, а), подобную
описанным выше, и элементы "память", образующие своего рода обратную
связь по отношению к комбинационной части.
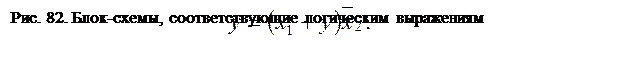 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.