Автоматизация управления установок с ДВС., страница 25

В разделе "Регуляторы прямого действия" было показано, что система с таким регулятором устойчива только при некоторой положительной степени неравномерности. Однако на практике нередки случаи, когда по условиям эксплуатации (обычно для привода генератора) необходимо обеспечить работу системы с нулевой или близкой к нулевой неравномерностью, а размеры и мощность двигателя делают нецелесообразным применение регулятора с гидроусилителем. Разрешить такое противоречие можно с помощью изодромной обратной связи, охватывающей измеритель скорости, который при нулевой неравномерности превращается в интегрирующее звено.

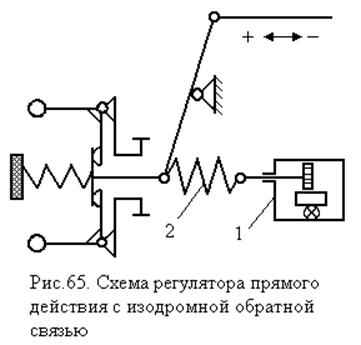Пример такой схемы показан на рис. 65. Главная пружина измерителя скорости настраивается на требуемую степень неравномерности. Для этого может использоваться также вспомогательная пружина типа показанной на
рис. 33, а. Обратную связь образует катаракт 1 с пружиной 2 (рис. 65). На устано-вившемся режиме давление в полостях катаракта одинаковое, его пружина не деформирована, и равновесие измерителя обеспечивается его главной пружиной. При изменении нагрузки изменяется частота вращения вала двигателя, что приводит к нарушению равновесия центробежной и восстанавливающей сил. Радиальное пере-мещение грузов смещает муфту измерителя и связанную с ним рейку топливного насоса. Одновременно деформируется пружина катаракта 2, создавая усилие, стремящееся вернуть измеритель к равновесному состоянию. После того, как моменты двигателя и сопротивления выравниваются вследствие изменения подачи топлива, изменение частоты вращения заканчивается. При отсутствии новых возмущений давление в полостях катаракта выравнивается, пружина катаракта 2 возвращается в недеформированное состояние и новое равновесие в измерителе возможно только в исходном положении грузов, т.е. при первоначальной частоте вращения. Таким образом, обеспечивается нулевая степень неравномерности системы регулирования при достаточной ее устойчивости.

2.11.5. Уравнения движения обратных связей.

Кинематические обратные связи описываются как суммирующее звено нулевого порядка. В этом легко убедиться, рассматривая зависимость между перемещениями муфты измерителя (z), золотника (s) и поршня (x) гидроусилителя при выполнении обратной связи в виде суммирующего рычага (рис. 59, а). Исходя из геометрических соображений, считая длины плеч рычага АВ = а и ВС = b,

z_н/(a + b) = s_н/b  и  s_н/a = x_н/(a + b), откуда

z_нb = x_нa = s_н(a+ b).

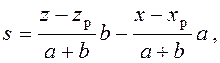
В общем случае следовательно,

s(a+ b) = (z-z_p)b- (х -x_p)а .

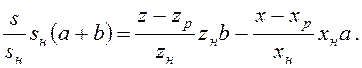
Для перехода к безразмерным величинам делим и умножаем все слагаемые на номинальное значение соответствующего параметра:

Вводим обозначения s/s_н = σ, (z - z_p)/z_н = η, (x - x_p)/x_н =ξ. Тогда уравнение жесткой обратной связи будет иметь вид σ = η - ξ (уравнение суммирующего звена).

Дифференциальное уравнение изодрома выведем, используя схему на рис. 60, б. Пусть площадь ведущего поршня F₁, ведомого F₂, давление в полости изодрома р, жесткость пружины ведомого поршня с и сила, действующая на ведомый поршень со стороны связанного с ним элемента регулятора - Р, перемещения ведущего и ведомого поршней соответственно х и у. Тогда движение поршней описывается двумя уравнениями.

Уравнение неразрывности, считая истечение через дросселирующий канал ламинарным,

F₁(dx/dt) - F₂(dy/dt) = ap, где а - коэффициент пропорциональности, учитывающий сечение дроссели-рующего канала и свойства жидкости.

Уравнение движения ведомого поршня (без учета сил инерции)

P + cy + k(dy/dt) = pF_{2 ,}

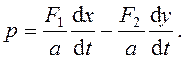
где k - коэффициент вязкого трения ведомого поршня. Из первого уравнения

При подстановке значения давления во второе уравнение, пренебрегая величиной силы Р как сравнительно малой, получим

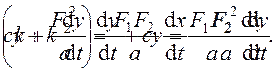
и далее

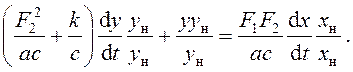
Для перехода к безразмерным величинам умножаем и делим, как обычно, каждое слагаемое на номинальный параметр, кроме того, делим обе части уравнения на с. Тогда

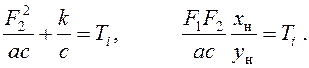
Вводим обозначения x/x_н = ξ, y/y_н = ζ,

Последние два выражения приравниваются друг другу за счет подбора номинальных величин х и у.

С учетом этих обозначений уравнение записывается как