Автоматизация управления установок с ДВС., страница 17

Регулятор должен быть спроектирован так, чтобы усилия, развиваемые при вращении грузов, и соответствующая им восстанавливающая сила были достаточны для преодоления противодействующих им сил, в первую очередь сил трения. Совершаемая при этом работа называется работоспособностью регулятора:

R=Ez_н .

При отсутствии достоверных данных о величинах сопротивлений работоспособность определяется по эмпирической формуле где λ_н - степень наддува; K - коэффициент; V_л - рабочий объём цилиндра в литрах, i - число цилиндров.

2.10. Динамика систем регулирования с регулятором

2.10.1. Дифференциальное уравнение движения
центробежного измерителя скорости

Дифференциальное уравнение измерителя имеет вид:

С=E+F_тp sign (dz/dt) + k(dz/dt) + m_r(d²z/dt²), где k - коэффициент вязкого трения; m_r - приведённая к муфте масса подвижных частей регулятора и связанных с ним деталей; z - перемещение муфты.

Приведение масс подвижных деталей производится на основе уравнения равенства кинетических энергий

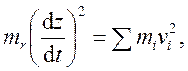
где m_i  - масса i-го элемента, v_i  - скорость перемещения этого элемента.

Рассмотрим некоторые наиболее типичные случаи.

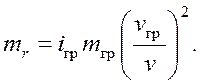
1) Приведенная масса грузов определяется как

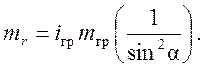
Для измерителя с грузами в виде шариков, перемещающихся между плоской и конусной тарелками (рис. 20, 25),

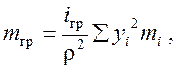
Для грузов в форме угловых рычагов (рис. 19), имеющих сложную форму, сечение груза предварительно разбивают на простые элементы, находят их центры тяжести и определяют приведенную массу по формуле:

где ρ - расстояние от оси качания груза до точки упора лапки груза в муфту;
y_i  - расстояние от центра тяжести элемента до оси качания.

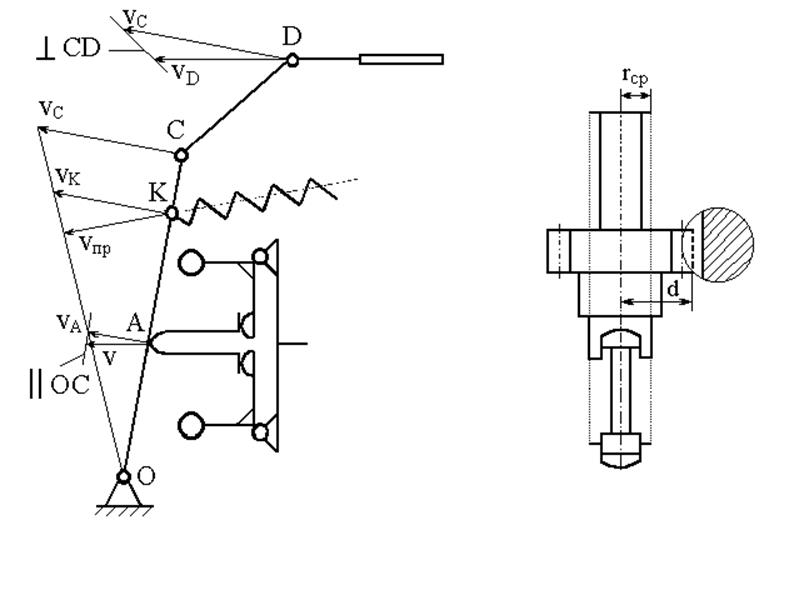
2) Рычаг рейки и связанные с ним детали (рис. 50)

а) Р ы ч а г. Рычаг ОС совершает вращательное движение относительно точки О. Его приведенная масса определяется как

m_rOC = I_OC/a² = m_OC(c²/3a²), где I_OC и m_OC  - момент инерции и масса рычага; а и с - длины отрезков ОА и ОС. б) П р у ж и н а. Масса пружины, приведенная к точке К, равна 1/3 ее действительной массы, причем ее скорость направлена по оси пружины. Для приведения к муфте эту массу следует умножить на квадрат отношения скоростей (V_пр/V)². Скорость пружины, как и другие скорости, находится из планов скоростей, как показано на рис. 50.

в) Т я г а. Массу тяги условно распределяют по точкам C и D пропорционально отношению расстояний от центра тяжести тяги до этих точек к длине тяги. Соответствующие скорости находятся из планов скоростей.

г) Д е т а л и  т о п л и в н о г о  н а с о с а. При перемещении муфты измерителя скорости рейка топливного насоса перемещается со скоростью V_D. К массе рейки прибавляются часть массы тяги, отнесенная к точке D, и условная масса, заменяющая момент инерции плунжеров. Для определения приведенной массы плунжеров эту деталь сложной формы заменяют цилиндром со средним радиусом r_ср. (рис. 51). Далее определяется момент инерции и масса плунжеров, приведенная к рейке m'_пл

I_пл = mr_ср²/2;    m'_пл = iI_пл /d²

Суммарная масса деталей, приведенная к рейке (сама рейка, плунжеры и часть массы тяги), приводится к муфте в соответствии с отношением квадрата скоростей V_D и V.

Приведенная к муфте масса регулятора определяется как сумма приведенных масс отдельных элементов.

Вывод дифференциального уравнения измерителя скорости производится, как и вывод уравнения объекта, с помощью метода малых отклонений. Учитывая, что восстанавливающая сила является функцией перемещения муфты Е = Е(z), а центробежная-функцией частоты вращения и перемещения муфты C = C(w,z), вблизи равновесной точки С_р = Е_р (параметры для этой точки обозначены индексом "р"):

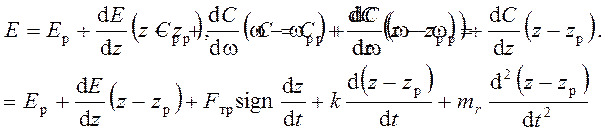
После подстановки этих значений дифференциальное уравнение приобретает вид:

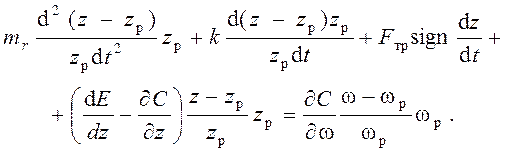
Далее переносим слагаемые, зависящие от z, в левую часть уравнения, зависящие от ω, в правую, а каждое слагаемое умножаем и делим на z_р или ω_р

Кроме того, обе части уравнения делим на 2E_р = 2С_р(ω) = 2А(z_р)ω_р².
Как показано в разделе "Статика центробежного измерителя скорости",
С(ω) = А(z)ω². Соответственно

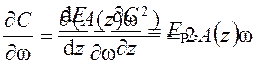
Учитывая также, что

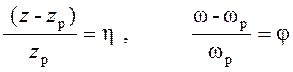
т.е. фактор устойчивости, вводим безразмерные параметры и получаем