Автоматизация управления установок с ДВС., страница 27

Первое из этих неравенств выполняется благодаря тому, что время вязкого трения и гидроусилителя в реальных конструкциях значительно выше времени измерителя. Можно обратить внимание также на то, что рационально устанавливать степень неравномерности измерителя выше коэффициента усиления, который, как показано выше, следует выбирать, исходя из требуемой степени неравномерности системы регулирования. Для анализа второго условия можно принять T_r² = 0. При этом обнаруживается, что устойчивость системы определяется отношением T_a/T_k, что указывает на необходимость уменьшения вязкого трения (в некоторых конструкциях регуляторов для этого предусматривается постоянное вращение втулки золотника). Кроме того, устойчивость повышается при увеличении степени неравномерности измерителя и системы в целом.

в) Системы с изодромной обратной связью (рис. 63).

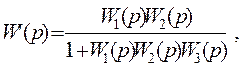
Условия устойчивости таких систем рассмотрим на примере системы с изодромной силовой обратной связью, поскольку по методике и результатам анализ систем с кинематической и силовой обратной связью вполне аналогичен. Структурная схема такой системы показана на рис. 66, в. Передаточные функции звеньев 0 (объект), 1 (измеритель) и 2 (гидроусилитель) те же, что для систем с жесткими обратными связями. Передаточная функция изодрома W₃(p) = T_ip/(T_ip+1). Передаточная функция регулятора (замкнутой цепи измерителя и гидроусилителя, охваченных изодромной обратной связью)

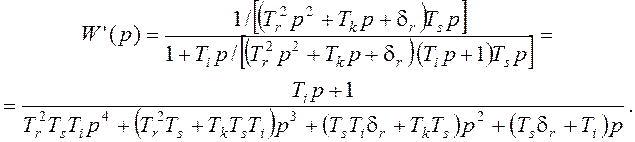
что при подстановке дает

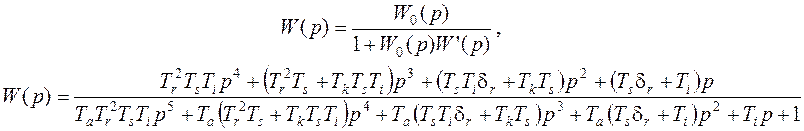
Передаточная функция системы

Подстановка р=0 показывает, что степень неравномерности системы равна нулю независимо от степени неравномерности измерителя и других параметров системы регулирования. Этот результат лишь подтверждает вывод, сделанный при описании работы систем с изодромной обратной связью.

Для упрощения анализа устойчивости данной системы пятого порядка принимаем T_r = T_k = 0. Тем самым порядок системы понижается до третьего с коэффициентами характеристического уравнения

a₀ = T_aT_sT_id_r,  a₁ = T_a(T_sd_r + T_i),  a₂ = T_i,  a₃=1.

Помимо обязательного условия устойчивости (положительности всех коэффициентов), которое выполняется при d_r>0, условием устойчивости системы третьего порядка является а₁а₂/а₀а₃>1. Подстановка значений коэффициентов дает

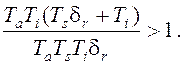
После почленного деления числителя на знаменатель это условие сводится к следующему:1 + T_i/(T_sd_r) > 1. Оно выполняется, если T_i  > 0, т.е. устойчивость системы обеспечивается самим фактом существования изодромной связи.

г) Система с регулятором прямого действия и изодромной обратной связью (рис. 65).

Структурная схема системы показана на рис. 66, г. Изодромная обратная связь с передаточной функцией W₂(p) охватывает измеритель скорости, следовательно, обратная связь является силовой. Передаточная функция этой цепочки

W'(p) = W₁(p)/(1 + W₁(p)W₂(p))

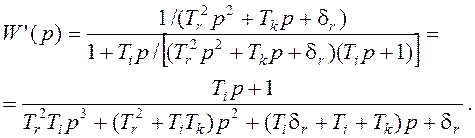
или

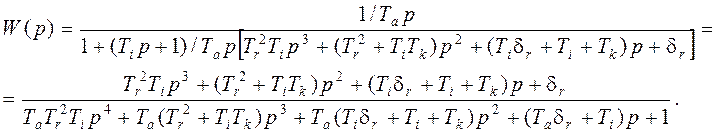
Передаточная функция системы W(p) = W₀(p)/(1 + W₀(p)W'(p)),т.е.

Очевидно, что в такой системе степень неравномерности равна степени неравномерности измерителя. Исходя из назначения регуляторов такой схемы, представляют интерес условия, при которых сохраняется устойчивость при нулевой степени неравномерности. В таком случае коэффициенты характеристического уравнения

a₀ = T_aT_iT_r²,a₁ = T_a(T_iT_k + T_r²),a₂ = T_a(T_k + T_i),a₃ = T_i,a₄ = 1.

Все эти коэффициенты положительны, если положительно время изодрома, следовательно, необходимое условие устойчивости выполняется даже при нулевой степени неравномерности. Согласно матрице Гурвица для системы четвертого порядка, условия устойчивости

а₁а₂ / (а₀а₃) > 1,a₃(a₁a₂-a₀a₃) / (a₁²a₄) > 1.

При подстановке значений коэффициентов первое из этих условий дает:

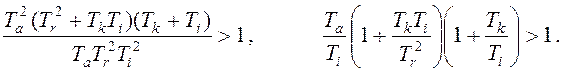Для гарантированного выполнения этого условия достаточно, чтобы время разгона двигателя было больше времени изодрома.

Второе условие:

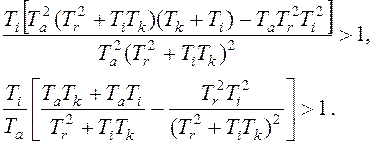
Проверка выполнения этого условия в числовых значениях для конкретной системы не составляет трудностей. Для качественной оценки влияния отдельных параметров системы регулирования на ее устойчивость можно принять время измерителя равным нулю (хотя в данном случае это допущение менее обоснованно, чем для систем с гидроусилителем). Тогда это условие устойчивости сводится к неравенству