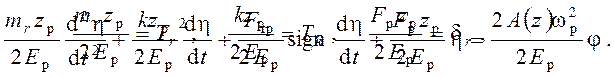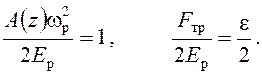
Автоматизация управления установок с ДВС., страница 18

Вводим обозначения:

где T_r - время измерителя, T_k - время вязкого трения, δ_r - степень неравномерности.

И учитываем, что

Тогда окончательный вид уравнения

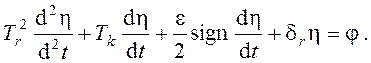
Слагаемое, учитывающее сухое трение,

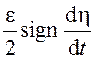
делает данное уравнение нелинейным. Если пренебречь им, то получим линейное дифференциальное уравнение, которое может быть преобразовано по Лапласу

(T_r²p² + T_k p + δ_r)η(p) = φ(p), откуда передаточная функция

W(p) = 1/(T_r²p² + T_k p + δ_r).

Передаточная функция показывает, что при положительной степени неравномерности δ_r измеритель скорости является звеном второго порядка, которое, как известно, может быть колебательным или апериодическим. При нулевой степени неравномерности это звено вырождается в последовательное соединение интегрирующего и апериодического звеньев.

2.10.2. Устойчивость и динамика систем регулирования скорости с регулятором прямого действия

Структурная схема системы с регулятором прямого действия показана на рис. 52. Здесь W₀(p) - объект регулирования (двигатель) с передаточной функцией

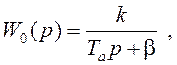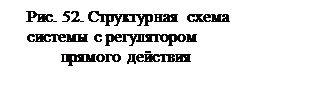
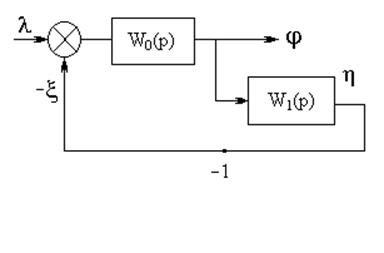
а W₁(p) - регулятор скорости, передаточная функция которого в данном случае совпадает с переда-точной функцией измерителя скорости, при этом время измерителя опре-деляется с учетом масс элементов топливного насоса, движущихся при перемещениях муфты измерителя. Его передаточная функция

W₁(p) = 1/(T_r²p² + T_k p + δ_r).

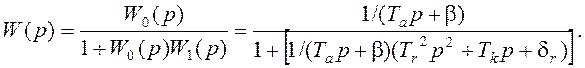
Усилительное звено с коэффициентом (-1) означает связь между выходом измерителя и рейкой топливного насоса.

Передаточная функция системы

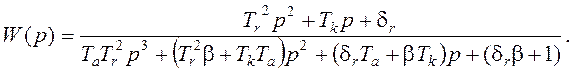
После приведения к общему знаменателю и упрощений передаточная функция

Из этой передаточной функции можно определить степень неравномерности системы:

δ = δ_r/(δ_rβ+1).

При нулевом самовыравнивании степень неравномерности системы равна степени неравномерности измерителя скорости. При положительном самовыравнивании степень неравномерности системы несколько меньше, однако при малых значениях степени неравномерности величина δ_rβ значительно меньше единицы, так что ее влияние незначительно.

Для анализа устойчивости рассматриваем характеристическое уравнение

Коэффициенты характеристического уравнения:

Необходимое условие устойчивости a₀>0, а₁>0, а₂>0, а₃>0 выполняется в соответствии с физическим смыслом коэффициентов характеристического уравнения, если δ_r >0. При нулевой степени неравномерности измерителя это условие устойчивости может быть выполнено, только если коэффициент самовыравнивания положительный. Этим, однако, устойчивость не гарантии-руется. Для точной оценки устойчивости системы необходимо обратиться к одному из критериев устойчивости, изученных в курсе "Теория автома-тического управления". В данном случае удобно воспользоваться критерием Гурвица, который для систем третьего порядка имеет вид

а₁а₂ - а₀а₃ > 0.

При подстановке значений коэффициентов это условие записывается как

(T_aT_k + βT_r²)(T_aδ_r + T_kβ) - T_aT_r²(βδ_r+1) > 0.

При анализе дифференциального уравнения дизеля как объекта регулирования отмечалось, что обычно коэффициентом самовыравнивания можно пренебречь. Тогда условие устойчивости упрощается:

T_aT_kδ_r > T_r²  или T_aT_kδ_r /T_r² > 1.

Отсюда вполне очевидно вытекает, что устойчивость системы регулирования скорости может быть повышена за счет увеличения, во-первых, степени неравномерности и, во-вторых, отношения времени разгона двигателя к квадрату времени измерителя скорости.

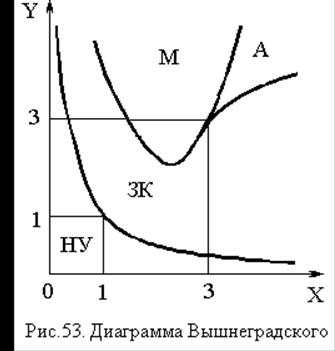Для более детального анализа влияния параметров системы регулирования на устойчивость и вид переходного процесса системы третьего порядка, каковой является рассматриваемая система регулирования, удобно использо-вать диаграмму Вышнеградского (рис. 53). Для этого характеристическое уравнение А(р) = 0 преобразуется к виду

q³ + Xq² + Yq + 1 = 0 ,

где X = (a₁/a₃)(a₃/a₀)^2/3, Y = (a₂/a₃)(a₃/a₀)^1/3.

Подстановка значений коэффициентов характеристического уравнения дает

X = (T_k/T_r)(T_a/T_r)^1/3,  Y = δ_r(T_a/T_r)^2/3.