Автоматизация управления установок с ДВС., страница 26

T_i(dζ/dt) + ζ = T_i(dξ/dt).

В преобразованном по Лапласу виде это уравнение принимает вид

(T_i p + 1) ζ(p) = T_i pξ(p), откуда передаточная функция

W(p) = T_i p/(T_i p + 1).

Таким образом, подтверждается, что изодром является реальным дифференцирующим звеном.

2.11.6. Статические и динамические свойства систем регулирования скорости с регуляторами с жесткими и изодромными обратными связями

Используя сведения о схемах регуляторов и о передаточных функциях обратных связей, изложенные в предыдущих разделах, рассмотрим статические свойства (степень неравномерности), устойчивость и динамику различных вариантов систем.

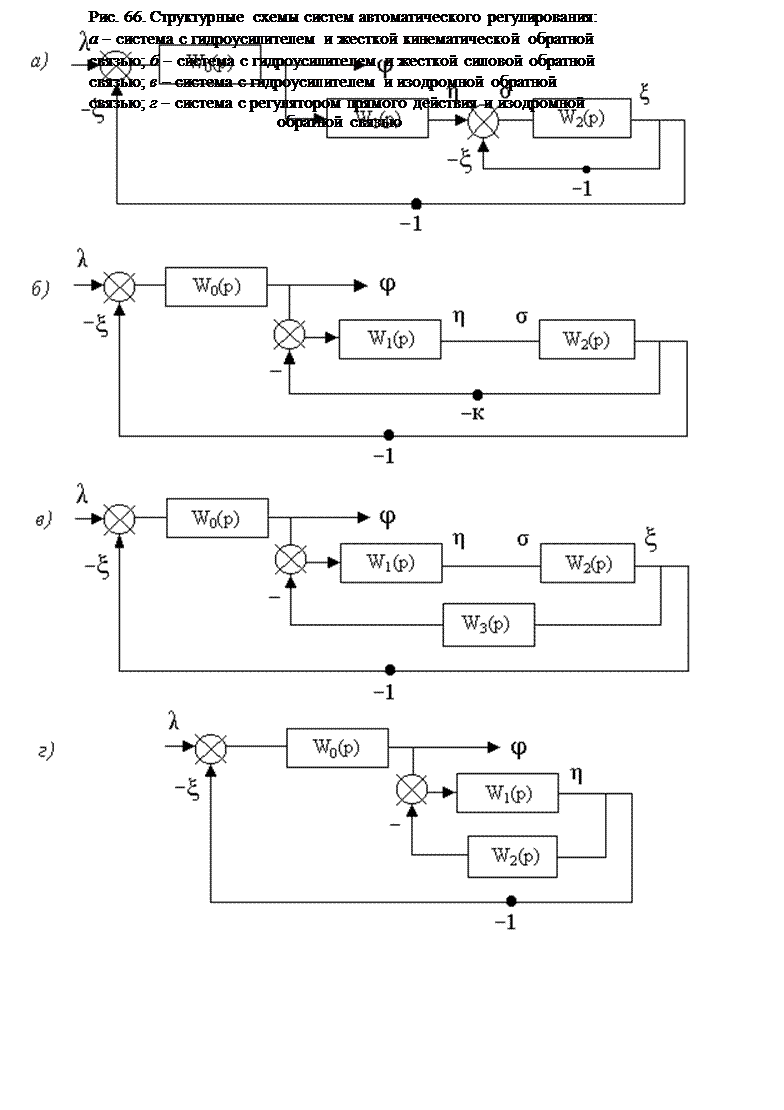
а) Система с гидроусилителем и жесткой кинематической обратной связью (рис. 61, а).

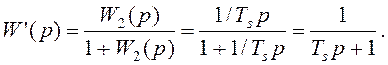
Структурная схема такой системы показана на рис. 66, а. Передаточные функции звеньев W₀(p) = 1/T_ap, W₁(p) = 1/(T_r² + T_kp + δ_r), W₂(p) = 1/T_sp. Жесткая обратная связь с коэффициентом усиления -1 подает выходной сигнал гидроусилителя (ход поршня) на его же вход, перемещая золотник. Передаточная функция звена W₂(p), охваченного обратной связью,

Таким образом, интегрирующее звено, охваченное обратной связью, преобразуется в апериодическое звено первого порядка.

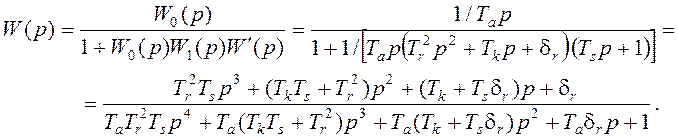
Передаточная функция системы в целом

Статическую ошибку (степень неравномерности) системы находим, подставляя в выражение для передаточной функции р=0. При этом выясняется, что δ = δ_r, т.е. степень неравномерности системы с жесткой кинематической обратной связью равна степени неравномерности измерителя скорости.

Для оценки устойчивости системы рассматриваем характеристическое уравнение A(p) = 0, где А(р) - знаменатель передаточной функции системы.

А(р) = а₀р⁴ + а₁р³ + а₂р² + а₃р + а_{4 ,}

где а₀ = T_aT_r²T_s;  a₁ = T_a(T_kT_s + T_r²);  a₂ = T_a(T_k + T_sδ_r);  a₃ = T_aδ_r;  a₄ = 1.

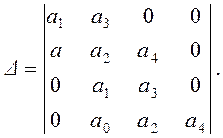
Очевидно, что необходимое условие устойчивости (положительное значение всех коэффициентов характеристического уравнения) здесь выполняется, если δ_r > 0. Следовательно, при данном типе обратной связи невозможно создание устойчивой системы с нулевой степенью неравномерности. Для полного анализа устойчивости рассматриваем матрицу Гурвица для системы четвертого порядка

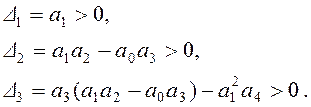
Согласно этой матрице, условия устойчивости, помимо необходимого, формулируются как

При подстановке значений коэффициентов во второе из этих условий получаем

T_a²(T_kT_s + T_r²)(T_k + T_s δ_r) - T_a²T_r²T_s δ_r > 0.

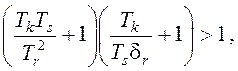
После преобразований это условие сводится к неравенству которое выполняется при любых положительных значениях времен звеньев и степени неравномерности.

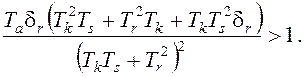
Третье условие после подстановки коэффициентов и упрощений дает неравенство

Для упрощения анализа можно считать, что время измерителя скорости в регуляторе с гидроусилителем, по крайней мере, на порядок ниже всех остальных и им можно пренебречь. Тогда это условие устойчивости сводится к следующему:

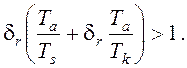
Очевидно, что при степени неравномерности 0,05 для выполнения этого условия необходимо, чтобы время разгона двигателя превышало время гидроусилителя по меньшей мере в 20 раз.

б) Система с гидроусилителем и жесткой силовой обратной связью
(рис. 61, б, в).

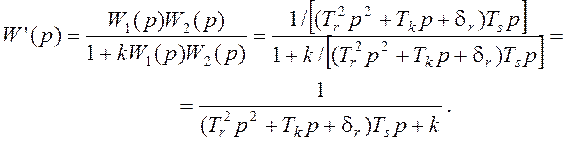
Структурная схема показана на рис. 66, б. Обратная связь здесь связывает перемещение поршня гидроусилителя с изменением усилия пружины измерителя скорости и охватывает поэтому два последовательно включенных звена: измеритель и гидроусилитель. Значения передаточных функций звеньев здесь такие же, как в предыдущем случае. Передаточная функция этой замкнутой цепочки

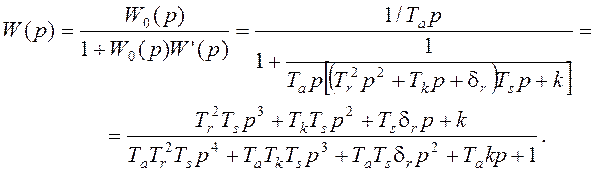
Передаточная функция системы

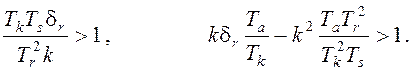
Степень неравномерности такой системы равна коэффициенту усиления обратной связи и не зависит от степени неравномерности измерителя скорости. Анализ на соответствие необходимому условию устойчивости показывает, что все времена звеньев, а также степень неравномерности измерителя и коэффициент усиления должны быть положительными. Критерии устойчивости, основанные на матрице Гурвица, дают следующие неравенства: